题目内容
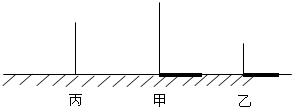如图所示，甲物体高4米，影长3米，乙物体高2米，影长4米，两物体相距5米．（1）在图中画出灯的位置，并画出丙物体的影子．
（2）若灯杆，甲、乙都与地面垂直并且在同一直线上，试求出灯的高度．
考点：中心投影
专题：
分析：（1）首先连接GA、HC并延长交于点O，从而确定点光源，然后连接OE并延长即可确定影子；
（2）OM⊥QH 设OM=x，BM=y，根据三角形相似列出比例式即可确定灯的高度．
（2）OM⊥QH 设OM=x，BM=y，根据三角形相似列出比例式即可确定灯的高度．
解答：
解：（1）点O为灯的位置，FM为丙物体的影子；
（2）作OM⊥QH 设OM=x，BM=y，
由△GAB∽△GOM得
=
即：
=
①，
由△CDH∽△OMH得
=
即：
=
②
由①②得，
x=4.8，y=0.6．
答灯的高度为4.8米．
解：（1）点O为灯的位置，FM为丙物体的影子；（2）作OM⊥QH 设OM=x，BM=y，
由△GAB∽△GOM得
| AB |
| OM |
| GB |
| GM |
即：
| 4 |
| x |
| 3 |
| 3+y |
由△CDH∽△OMH得
| CD |
| OM |
| DH |
| HM |
即：
| 2 |
| x |
| 4 |
| 4+5+y |
由①②得，
x=4.8，y=0.6．
答灯的高度为4.8米．
点评：本题考查了中心投影的知识，解题的关键是根据两个物体及其影子确定点光源，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC的边AC与⊙O相交于C、D两点，且经过圆心O，边AB与⊙O相切，切点为B．已知∠A=30°，则∠C的大小是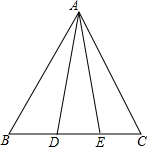
如图，在△ABC中，点D、E在边BC上，现有①AB=AC，②AD=AE，③BD=CE．请你用其中两个作为条件，余下一个作为结论，编写一道数学问题，并写出解答过程．
如图，在△ABC中，∠A＜90°，∠C=30°，AB=4，BC=6，E为AB的中点，P为AC边上一动点，将△ABC绕点B逆时针旋转a角（0°＜a≤360°）得到△A1B1C1，点P的对应点为P1，连EP1，在旋转过程中，线段EP1的长度的最小值是（ ）
如图，在正方形ABCD中，F是AD边的中点，E是BA延长线上一点，且AE=
如图所示：正方形网格中的四边形ABCD，若小方格的边长为1，则四边形ABCD的面积是
