题目内容

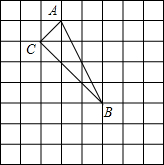每个小正方形的边长为1．
（1）求△ABC的面积；
（2）判断△ABC的形状．
考点：勾股定理,三角形的面积,勾股定理的逆定理
专题：网格型
分析：（1）根据图形，则三角形的面积等于矩形的面积减去3个直角三角形的面积．
（2）根据勾股定理可计算出AC，BC，AB的长，进而可判断△ABC的形状．
解答：解：（1）△ABC的面积=4×3-
1
2
×（1×1+2×3+3×3）=4；
（2）由勾股定理可得：AC=
2
，BC=3
2
，AB=
20
=2
5
，
所以AC2+BC2=AB2=20，
即△ABC的形状是直角三角形．
点评：本题考查了勾股定理以及其逆定理的运用，解题的关键是善于把不规则图形的面积转化为规则图形的面积．
练习册系列答案
相关题目
实验中学七年级（2）班有学生56人，已知男生人数比女生人数的2倍少11人，求男生和女生各多少人？下面设未知数的方法，合适的是（　　）
A、设总人数为x人
B、设男生比女生多x人
C、设男生人数是女生人数的x倍
D、设女生人数为x人
已知b=
4-a
+
a-4
+5，
（1）求a的值；
（2）求(
a
+
b
)2006(
a
-
b
)2007的值．
如图，平面直角坐标系中，已知A（-2，0），B（2，0），C（6，0），D为y轴正半轴上一点，且∠ODB=30°，延长DB至E，使BE=BD．P为x轴正半轴上一动点（P在C点右边），M在EP上，且∠EMA=60°，AM交BE于N．
（1）求证：BE=BC；
（2）求证：∠ANB=∠EPC；
（3）当P点运动时，求BP-BN的值．
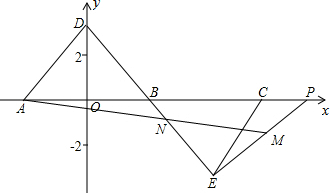
已知在△FEC中，∠ACB=90°，AC=BC，∠ECF=135°，BE=x，BF=y．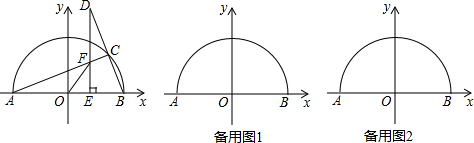
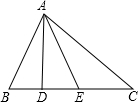（1）求证：∠ECA=∠F； 
（2）若AE=2，求y与x的函数关系式．
国家规定个人发表文章、出版图书所获稿费的纳税计算方法是：
a．稿费低于800元的不纳税；
b．稿费高于800元，又低于4000元的应缴纳超过800元那部分稿费的14%的税（如稿费为1000元，则应纳税（1000-800）×14%=28元）；
c．稿费为4000元以上的应缴纳全部稿费的11%的税．
试根据上述纳税的计算方法解答
①李老师获得的稿费为2200元，则应纳税
 
元，李老师获得的稿费为4500元，则应纳税
 
元．
②若李老师获得稿费后纳税420元，请你算-算李老师实得这笔稿费是多少元？
如图，在平面直角坐标系中，点A、B的坐标分别为（-5，0）和（5，0），以AB为直径在x轴的上方作半圆O，点C是该半圆上第一象限内的一个动点，连结AC、BC，并延长BC至点D，使BC=CD，过点D作x轴的垂线，分别交x轴、线段AC于点E、F，E为垂足，连结OF．
（1）当∠CAB=30°时，求弧BC的长；
（2）当AE=6时，求弦BC的长；
（3）在点C运动的过程中，是否存在以点O、E、F为顶点的三角形与△DEB相似？若存在，请求出此时E点的坐标；若不存在，请说明理由．
如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=80°，∠C=46°
（1）你会求∠DAE的度数吗？
（2）你能发现∠DAE与∠B、∠C之间的关系吗？
（3）若只知道∠B-∠C=20°，你能求出∠DAE的度数吗？
（4）∠AED是哪个三角形的外角？
已知一次函数y1=-
b
4
x-4，与y2=2ax+4a+b
（1）求a、b为何值时，两函数的图象重合？
（2）如果它们图象的交点为 P（-1，3），试确定方程组
y=-
b
4
x-4
y=2ax+4a+b
的解并求a、b的值？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网