题目内容
 如图所示,过正方形ABCD的顶点A作对角线BD的平行线,在这条直线上取一点E,使BD=ED,且DE与AB交于点F,证明:BE=BF.
如图所示,过正方形ABCD的顶点A作对角线BD的平行线,在这条直线上取一点E,使BD=ED,且DE与AB交于点F,证明:BE=BF.考点:正方形的性质,等腰三角形的性质,含30度角的直角三角形
专题:证明题
分析:过A作AG垂直BD于G,过E作EH垂直BD于H.先证明四边形AEHG为矩形,根据矩形和正方形的性质得到AG=EH=
DB,进一步得到EH=
DE,由直角三角形EHD中,EH为斜边DE的一半得到∠EDH=30°,再根据等腰三角形的性质和角的和差关系得到∠BFE=∠DEB,从而得到BE=BF.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明: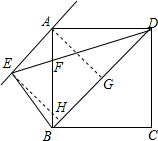 过A作AG垂直BD于G,过E作EH垂直BD于H.
过A作AG垂直BD于G,过E作EH垂直BD于H.
∵AE∥DB,
∴四边形AEHG为矩形,
∴AG=EH=
DB,
又∵DE=DB,
∴EH=
DE,
∴∠EDH=30°(直角三角形EHD中,EH为斜边DE的一半)
又∵BD=DE,
∴∠DEB=∠EBD=(180°-30°)÷2=75°,
又∵∠BFE=∠FBD+∠FDB=45°+30°=75°=∠DEB,
∴BE=BF.
 过A作AG垂直BD于G,过E作EH垂直BD于H.
过A作AG垂直BD于G,过E作EH垂直BD于H.∵AE∥DB,
∴四边形AEHG为矩形,
∴AG=EH=
| 1 |
| 2 |
又∵DE=DB,
∴EH=
| 1 |
| 2 |
∴∠EDH=30°(直角三角形EHD中,EH为斜边DE的一半)
又∵BD=DE,
∴∠DEB=∠EBD=(180°-30°)÷2=75°,
又∵∠BFE=∠FBD+∠FDB=45°+30°=75°=∠DEB,
∴BE=BF.
点评:考查了矩形的判定和性质,正方形的性质,含30度角的直角三角形的性质,等腰三角形的性质,关键是作出辅助线.

练习册系列答案
相关题目
若|x-2|-x+2=0,那么( )
| A、x=2 | B、x≥2 |
| C、x≤2 | D、-2≤x≤2 |
 已知在△FEC中,∠ACB=90°,AC=BC,∠ECF=135°,BE=x,BF=y.
已知在△FEC中,∠ACB=90°,AC=BC,∠ECF=135°,BE=x,BF=y.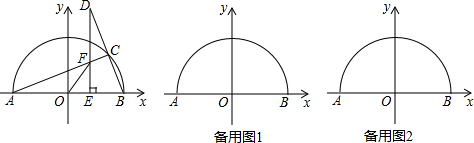
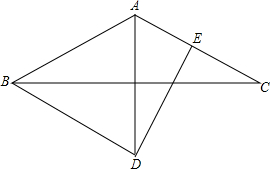 如图,△ABC是等腰三角形,AB=AC,∠CBD=30°,DE垂直平分AC,求证:AB=AD.
如图,△ABC是等腰三角形,AB=AC,∠CBD=30°,DE垂直平分AC,求证:AB=AD.