题目内容
 如图,梯形ABCD中AD∥BC,∠B=90,P为DC上一点,PE⊥AB、PF⊥BC垂足分别为E、F,AD=1,AB=2,BC=5,BF=x,矩形EBFP面积为y,求y与x之间的函数关系式.
如图,梯形ABCD中AD∥BC,∠B=90,P为DC上一点,PE⊥AB、PF⊥BC垂足分别为E、F,AD=1,AB=2,BC=5,BF=x,矩形EBFP面积为y,求y与x之间的函数关系式.考点:相似三角形的判定与性质,根据实际问题列二次函数关系式,梯形
专题:
分析:首先过点D作DG⊥BC于点G,进而得出四边形ABGD为矩形,再得出△CPF∽△CDG,进而求出y与x的函数关系式即可.
解答: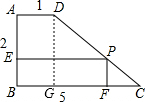 解:过点D作DG⊥BC于点G,则四边形ABGD为矩形,
解:过点D作DG⊥BC于点G,则四边形ABGD为矩形,
故DG=AB=2,BG=AD=1,
则CG=BC-BG=5-1=4,
∵BC=5,BF=x,
∴CF=BC-BF=5-x,
∵四边形EBFP为矩形,
∴PF∥AB∥DG,
∴△CPF∽△CDG,
∴
=
,即
=
,
∴PF=
(5-x),
∴y=BF×PF=x×
(5-x)=-
x2+
x,
故y与x之间的函数关系式为:y=-
x2+
x(1≤x<5).
 解:过点D作DG⊥BC于点G,则四边形ABGD为矩形,
解:过点D作DG⊥BC于点G,则四边形ABGD为矩形,故DG=AB=2,BG=AD=1,
则CG=BC-BG=5-1=4,
∵BC=5,BF=x,
∴CF=BC-BF=5-x,
∵四边形EBFP为矩形,
∴PF∥AB∥DG,
∴△CPF∽△CDG,
∴
| PF |
| DG |
| FC |
| GC |
| PF |
| 2 |
| 5-x |
| 4 |
∴PF=
| 1 |
| 2 |
∴y=BF×PF=x×
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
故y与x之间的函数关系式为:y=-
| 1 |
| 2 |
| 5 |
| 2 |
点评:此题主要考查了相似三角形的判定与性质以及矩形的性质,得出△CPF∽△CDG是解题关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
代数式2(x-y)的意义是( )
| A、x的2倍与y的差 |
| B、x减去y的2倍 |
| C、y与x的差的2倍 |
| D、x与y的差的2倍 |
用两根长12cm的铁丝分别围成正方形和长与宽之比为2:1的长方形,则长方形和正方形的面积依次为( )
| A、9cm2和8cm2 |
| B、8cm2和9cm2 |
| C、32cm2和36cm2 |
| D、36cm2和32cm2 |
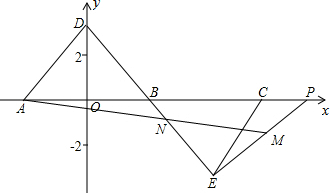
 已知在△FEC中,∠ACB=90°,AC=BC,∠ECF=135°,BE=x,BF=y.
已知在△FEC中,∠ACB=90°,AC=BC,∠ECF=135°,BE=x,BF=y.