题目内容
11.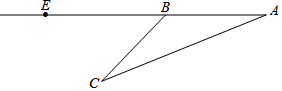 日前一渔船在南海打渔时遇险,并立即拨打了求救电话,警方接到电话立即派出直升机前去营救.飞机在空中A点看到渔船C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见渔船C的俯角为45°,已知飞机的飞行速度为3150米/分.(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)
日前一渔船在南海打渔时遇险,并立即拨打了求救电话,警方接到电话立即派出直升机前去营救.飞机在空中A点看到渔船C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见渔船C的俯角为45°,已知飞机的飞行速度为3150米/分.(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)(1)求渔船到直升机航线的垂直距离为多少米?
(2)在B点时,机组人员接到指挥部电话,8分钟后该海域将有较大风浪,为了能及时营救船上被困人员,机组人员决定飞行到C点的正上方立即空投设备,将受困人员救回机舱(忽略风速对设备的影响)已知设备在空中降落与上升的速度均为700米/分,设备救人本身需要6分钟,请问能否在风浪来临前将被困人员救回机舱?请说明理由.
分析 (1)设CD=x米,根据题意得到BD=x米,根据正切的概念列式计算即可;
(2)计算出直升飞机往返需要的时间与8分钟进行比较即可.
解答 解:(1)设CD=x米,
∵∠DBC=45°,
∴BD=x米,
由题意得,AB=3150×$\frac{16}{60}$=840米,
tanA=$\frac{CD}{AD}$,即$\frac{x}{x+840}$=0.3,
解得,x=360米
∴残骸到直升机航线的垂直距离CD为360米;
(2)直升飞机从B到D需要的时间:$\frac{360}{3150}$≈0.11分,
直升飞机从D到C和返回需要的时间:$\frac{720}{700}$≈1分,
0.11+1+6=7.11<8,
∴能在风浪来临前将残骸抓回机舱.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,正确理解题意、灵活运用锐角三角函数的概念是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
2.二次函数y=(x-1)2-2的顶点坐标是( )
| A. | (1,-2) | B. | (-1,2) | C. | (-1,-2) | D. | (1,2) |
19.某蔬菜生产基地经市场调查,对种植的A、B、C三种蔬菜的成本与售价情况统计如表:
并且从市场调研中总结得知:该基地的蔬菜C的种植面积一般是蔬菜B种植面积的2倍,生产基地要按照这个规律种植,才不至于滞销.现知道基地共有用地200亩,蔬菜A每亩产量为3吨,蔬菜B每亩产量为5吨,蔬菜C每亩产量为7吨.若设种植蔬菜B为x亩,基地假设把生产的蔬菜都能销售出去,其利润为y元.
(1)求y与x之间的函数关系式;
(2)根据市场行情,蔬菜A的种植不能多于50亩,求该蔬菜生产基地在这次种植中能获得的最大利润.
| 蔬菜品种 | A | B | C |
| 成本(元/吨) | 3000 | 2200 | 1500 |
| 售价(元/吨) | 7000 | 4000 | 3200 |
(1)求y与x之间的函数关系式;
(2)根据市场行情,蔬菜A的种植不能多于50亩,求该蔬菜生产基地在这次种植中能获得的最大利润.
16.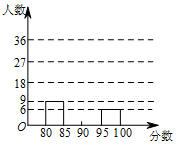 为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:
为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:
(1)请在图中补全频数分布直方图;
(2)抽取的这部分参赛同学成绩的中位数落在哪个分数段?
(3)如果该校参加人数1000人,请估计分数在95≤x<100段的人数约为多少?
 为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:
为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:| 分数段 | 频数 | 频率 |
| 80≤x<85 | 9 | 0.15 |
| 85≤x<90 | m | 0.45 |
| 90≤x<95 | ■ | ■ |
| 95≤x<100 | 6 | n |
(2)抽取的这部分参赛同学成绩的中位数落在哪个分数段?
(3)如果该校参加人数1000人,请估计分数在95≤x<100段的人数约为多少?
1.下列计算正确的是( )
| A. | (ab)4÷(ab3)=ab | B. | a10÷(a5÷a3)=a8 | C. | xm+3÷xm+1=x3 | D. | (x3n÷xn)÷x2n=x |
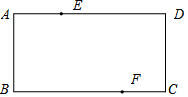 如图,已知矩形ABCD,分别在边AD,BC上找一点E和F,使四边形DEBF是菱形.
如图,已知矩形ABCD,分别在边AD,BC上找一点E和F,使四边形DEBF是菱形. 如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.求证:AM=DM.
如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.求证:AM=DM.