题目内容
10. 实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,绝对值最小的是( )| A. | a | B. | b | C. | c | D. | d |
分析 根据哪个数离原点越近,则哪个数的绝对值越小,判断出这四个数中,绝对值最小的是哪个即可.
解答 解:∵c=0,在数轴上对应点是原点,
∴这四个数中,绝对值最小的是c.
故选:C.
点评 此题主要考查了实数大小比较的方法,以及数轴的特征和应用,要熟练掌握,解答此题的关键是要明确:哪个数离原点越近,则哪个数的绝对值越小.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
20.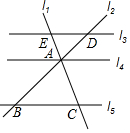 如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )
如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )
 如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )
如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )| A. | $\frac{EA}{AC}$=$\frac{DA}{AB}$ | B. | $\frac{BA}{BD}$=$\frac{CA}{CE}$ | C. | $\frac{CA}{CE}$=$\frac{DA}{DB}$ | D. | $\frac{EA}{EC}$=$\frac{DA}{DB}$ |
18.下列关于单项式$-\frac{{3x{y^2}}}{5}$的说法中,正确的是( )
| A. | 系数是3,次数是2 | B. | 系数是$-\frac{3}{5}$,次数是2 | ||
| C. | 系数是$\frac{3}{5}$,次数是3 | D. | 系数是$-\frac{3}{5}$,次数是3 |
5.某校初三学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是甲班和乙班成绩最好的5名学生的比赛成绩.
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)甲班的优秀率为60%,则乙班的优秀率为40%;
(2)甲班比赛成绩的方差S甲2=$\frac{26}{5}$,求乙班比赛成绩的方差;
(3)根据以上信息,你认为应该把团体第一名的奖状给哪一个班?简述理由.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 100 | 98 | 102 | 97 | 103 | 500 |
| 乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
(1)甲班的优秀率为60%,则乙班的优秀率为40%;
(2)甲班比赛成绩的方差S甲2=$\frac{26}{5}$,求乙班比赛成绩的方差;
(3)根据以上信息,你认为应该把团体第一名的奖状给哪一个班?简述理由.
2.已知一个等腰三角形的一个内角是50°,则这个等腰三角形的另外两个内角度数分别是( )
| A. | 50°,80° | B. | 65°,65° | ||
| C. | 50°,80°或65°,65° | D. | 无法确定 |
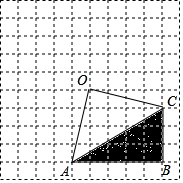 如图,在网格中有一个四边形图案.
如图,在网格中有一个四边形图案.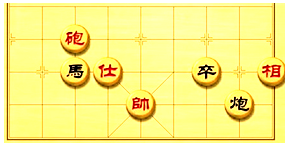 象棋在中国有着三千多年的历史,属于二人对抗性游戏的一种.由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.如图是一方的棋盘,如果“马”的坐标是(-2,2),它是抛物线y=ax2(a≠0)上的一个点,那么下面哪个棋子在该抛物线上( )
象棋在中国有着三千多年的历史,属于二人对抗性游戏的一种.由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.如图是一方的棋盘,如果“马”的坐标是(-2,2),它是抛物线y=ax2(a≠0)上的一个点,那么下面哪个棋子在该抛物线上( ) 如图所示,若∠DBE=78°,则∠A+∠C+∠D+∠E=102°.
如图所示,若∠DBE=78°,则∠A+∠C+∠D+∠E=102°.