题目内容
16.矩形ABCD的两条对角线AC、BD相交于点O,∠AOB=60°,OA=3,则这个矩形的面积为9$\sqrt{3}$.分析 由矩形的性质和已知条件得出△AOB是等边三角形,得出AB=OA=3,得出AC,由勾股定理求出BC,由矩形的面积公式即可得出结果.
解答 解:如图所示: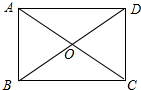
∵四边形ABCD是矩形,
∴OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,∠ABC=90°,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=3,
∴AC=2OA=6,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴矩形ABCD的面积=AB•BC=3×3$\sqrt{3}$=9$\sqrt{3}$.
故答案为:9$\sqrt{3}$.
点评 本题考查了矩形的性质、等边三角形的判定与性质、勾股定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
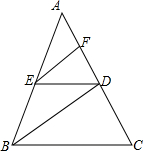 如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,
如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,