题目内容
14.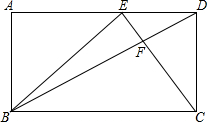 如图所示,长方形ABCD中,点E为AD边上的一点,连接BD,CE相交于点F,三角形EFD、三角形DFC的面积分别10,25平方厘米.
如图所示,长方形ABCD中,点E为AD边上的一点,连接BD,CE相交于点F,三角形EFD、三角形DFC的面积分别10,25平方厘米.(1)求三角形BEF的面积;
(2)求四边形ABFE的面积.
分析 (1)由DE∥BC,推出△DEF∽△BCF,推出$\frac{DE}{CB}$=$\frac{DF}{BF}$=$\frac{EF}{FC}$,由$\frac{{S}_{△EFD}}{{S}_{△DFC}}$=$\frac{EF}{FC}$=$\frac{10}{25}$=$\frac{2}{5}$,推出$\frac{DE}{BC}$=$\frac{DF}{BF}$=$\frac{2}{5}$,由S△DEF=10,推出S△BEF=25.
(2)由S△DEF=10,S△BEF=25,推出S△BED=35,由DE:DA=2:5,推出DE:AE=2:3,推出S△ABE=$\frac{105}{2}$,由此即可解决问题.
解答 解:(1)∵DE∥BC,
∴△DEF∽△BCF,
∴$\frac{DE}{CB}$=$\frac{DF}{BF}$=$\frac{EF}{FC}$,
∵$\frac{{S}_{△EFD}}{{S}_{△DFC}}$=$\frac{EF}{FC}$=$\frac{10}{25}$=$\frac{2}{5}$,
∴$\frac{DE}{BC}$=$\frac{DF}{BF}$=$\frac{2}{5}$,
∵S△DEF=10,
∴S△BEF=25,
(2)∵S△DEF=10,S△BEF=25,
∴S△BED=35,
∵DE:DA=2:5,
∴DE:AE=2:3,
∴S△ABE=$\frac{105}{2}$,
∴四边形ABFE的面积=$\frac{105}{2}$+25=$\frac{155}{2}$
点评 本题考查矩形的性质、相似三角形的判定和性质.三角形的面积等知识,解题的关键是掌握异底同高的三角形的面积之比等于底的比,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +(a-3b)2=2a2+5b2
+(a-3b)2=2a2+5b2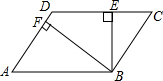 如图,?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,CE=3,DF=4,∠EBF=60°,求?ABCD的面积.
如图,?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,CE=3,DF=4,∠EBF=60°,求?ABCD的面积.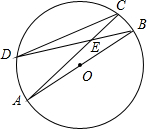 如图,AB是⊙O的直径,弦AC,BD交于点E,且tan∠AED=$\frac{1}{2}$,则$\frac{AB}{DC}$的值是$\frac{\sqrt{5}}{2}$.
如图,AB是⊙O的直径,弦AC,BD交于点E,且tan∠AED=$\frac{1}{2}$,则$\frac{AB}{DC}$的值是$\frac{\sqrt{5}}{2}$.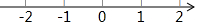 如图所示,数轴上的点A,B,C依次表示三个实数:1$\frac{1}{2}$,-1$\frac{1}{2}$,$\sqrt{3}$.
如图所示,数轴上的点A,B,C依次表示三个实数:1$\frac{1}{2}$,-1$\frac{1}{2}$,$\sqrt{3}$.