题目内容
9.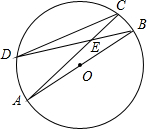 如图,AB是⊙O的直径,弦AC,BD交于点E,且tan∠AED=$\frac{1}{2}$,则$\frac{AB}{DC}$的值是$\frac{\sqrt{5}}{2}$.
如图,AB是⊙O的直径,弦AC,BD交于点E,且tan∠AED=$\frac{1}{2}$,则$\frac{AB}{DC}$的值是$\frac{\sqrt{5}}{2}$.
分析 连接AD,根据圆周角定理得到∠ADB=90°,根据正切的概念、勾股定理求出$\frac{AE}{DE}$=$\frac{\sqrt{5}}{2}$,根据相似三角形的判定定理和性质定理计算即可.
解答 解:连接AD,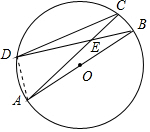
∵AB是⊙O的直径,
∴∠ADB=90°,
∵tan∠AED=$\frac{1}{2}$,
∴$\frac{AD}{DE}$=$\frac{1}{2}$,
由勾股定理得,$\frac{AE}{DE}$=$\frac{\sqrt{5}}{2}$,
∵∠C=∠B,∠DEC=∠AEB,
∴△AEB∽△DEC,
∴$\frac{AB}{DC}$=$\frac{AE}{DE}$=$\frac{\sqrt{5}}{2}$,
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查的是相似三角形的判定和性质、正切的概念、勾股定理的应用,掌握相似三角形的判定定理和性质定理、圆周角定理是解题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 如图,点C是以AB为直径的⊙O上一点,CD是⊙O切线,D在AB的延长线上,作AE⊥CD于E.
如图,点C是以AB为直径的⊙O上一点,CD是⊙O切线,D在AB的延长线上,作AE⊥CD于E.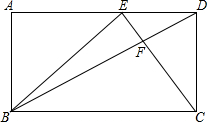 如图所示,长方形ABCD中,点E为AD边上的一点,连接BD,CE相交于点F,三角形EFD、三角形DFC的面积分别10,25平方厘米.
如图所示,长方形ABCD中,点E为AD边上的一点,连接BD,CE相交于点F,三角形EFD、三角形DFC的面积分别10,25平方厘米.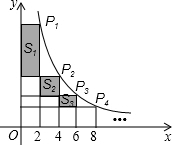 如图,在反比例函数y=$\frac{10}{x}$(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=10-$\frac{10}{n+1}$(用含n的代数式表示)
如图,在反比例函数y=$\frac{10}{x}$(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=10-$\frac{10}{n+1}$(用含n的代数式表示)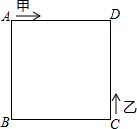 如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若甲的速度是乙的速度的3倍,则它们第2017次相遇在边CD上.
如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若甲的速度是乙的速度的3倍,则它们第2017次相遇在边CD上.