Question

13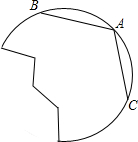．将图中的破轮子复原，已知弧上三点A，B，C．
（1）画出该轮的圆心；
（2）若△ABC是等腰三角形，底边BC=16cm，腰AB=10cm，求圆片的半径R．

Answer 1

分析 （1）根据垂径定理，分别作弦AB和AC的垂直平分线交点即为所求；
（2）连接AO，OB，利用垂径定理和勾股定理可求出圆片的半径R．

解答 解：（1）如图所示：分别作弦AB和AC的垂直平分线交点O即为所求的圆心；

（2）连接AO，OB，
∵BC=16cm，
∴BD=8cm，
∵AB=10cm，
∴AD=6cm，
设圆片的半径为R，在Rt△BOD中，OD=（R-6）cm，
∴R²=8²+（R-6）²，
解得：R=$\frac{25}{3}$cm，
∴圆片的半径R为$\frac{25}{3}$cm．

点评 本题主要考查了垂径定理的推论，我们可以把垂径定理的题设和结论这样叙述：一条直线①过圆心，②垂直于弦，③平分弦，④平分优弧，⑤平分劣弧．在应用垂径定理解题时，只要具备上述5条中任意2条，则其他3条成立．