题目内容
5．
如图，在⊙O中，$\widehat{AB}$=2$\widehat{CD}$，则下列结论正确的是（ ）| A． | AB＞2CD | B． | AB=2CD | C． | AB＜2CD | D． | 以上都不正确 |
分析 首先取$\widehat{AB}$的中点E，连接AE，BE，由在⊙O中，$\widehat{AB}$=2$\widehat{CD}$，可证得$\widehat{AE}$=$\widehat{BE}$=$\widehat{CD}$，即可得AE=BE=CD，然后由三角形的三边关系，求得答案．
解答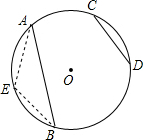 
解：取$\widehat{AB}$的中点E，连接AE，BE，
∵在⊙O中，$\widehat{AB}$=2$\widehat{CD}$，
∴$\widehat{AE}$=$\widehat{BE}$=$\widehat{CD}$，
∴AE=BE=CD，
∵AE+BE＞AB，
∴2CD＞AB．
故选C．
点评 此题考查了弧与弦的关系以及三角形的三边关系．注意在同圆或等圆中，同弧或等弧，所对的弦相等．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
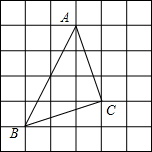如图所示的方格纸中，每一格小正方形的边长均为1，小莉画出一个等腰直角三角形ABC，她画得对吗？请你设法验证一下，并与同伴交流各自的方法．
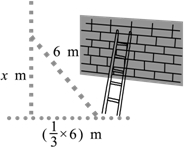生活表明，靠墙摆放梯子时，若梯子底端离墙的距离为梯子长度的三分之一，则梯子比较稳定．现有一长度为6m的梯子，当梯子稳定摆放时，它的顶端最多能到达多高？（精确到0.1m）
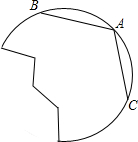将图中的破轮子复原，已知弧上三点A，B，C．
20．
在如图所示的象棋盘上，建立适当的平面直角坐标系，使“炮”位于点（-1，1）上，“相”位于点（4，-2）上，则“帅”位于点（ ）
在如图所示的象棋盘上，建立适当的平面直角坐标系，使“炮”位于点（-1，1）上，“相”位于点（4，-2）上，则“帅”位于点（ ）| A． | （-3，3） | B． | （-2，2） | C． | （3，-3） | D． | （2，-1） |
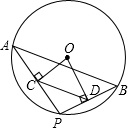如图，点A，B是⊙O上两点，AB=10，点P是⊙O上的动点（P与A，B不重合），连接AP，PB，过点O分别作OC⊥AP于点C，OD⊥PB于点D，则CD=5．
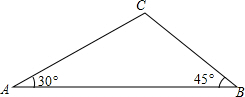如图，在△ABC中，∠A=30°，∠B=45°，AB=12+12$\sqrt{3}$，求△ABC的面积．
如图，已知正方形ABCD的边长为2，若将线段BD绕点B旋转后，点D落在CB的延长线上的D′处，试求tan∠BAD′的值．