题目内容
3. 如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,点B的坐标为(3,-$\frac{3}{2}$)直线l1,l2交于点C.
如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,点B的坐标为(3,-$\frac{3}{2}$)直线l1,l2交于点C.(1)求直线l2的函数关系式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,求出点P的坐标;
(4)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.
分析 (1)设直线l2的解析式为y=kx+b,把A与B的坐标代入求出k与b的值,即可确定出l2的解析式;
(2)由A与D坐标求出AD的长,C纵坐标的绝对值为高,求出三角形ADC面积即可;
(3)根据直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,得到P纵坐标等于C纵坐标的绝对值,将C纵坐标绝对值代入l2的解析式求出横坐标,确定出P坐标即可;
(4)在坐标平面内存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形,如图所示,分别求出H坐标即可.
解答 解:(1)设直线l2的解析式为y=kx+b,
把A(4,0),B(3,-$\frac{3}{2}$)代入得:$\left\{\begin{array}{l}{4k+b=0}\\{3k+b=-\frac{3}{2}}\end{array}\right.$,
解得:k=$\frac{3}{2}$,b=-6,
则直线l2的解析式为y=$\frac{3}{2}$x-6;
(2)对于直线l1:y=-3x+3,令y=0,得到x=1,即D(1,0),
联立得:$\left\{\begin{array}{l}{y=-3x+3}\\{y=\frac{3}{2}x-6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,即C(2,-3),
∵A(4,0),C(2,-3),D(1,0),
∴AD=3,C纵坐标的绝对值为3,
则S△ADC=$\frac{1}{2}$×3×3=$\frac{9}{2}$;
(3)由题意得到P纵坐标为3,
把y=3代入l2的解析式为y=$\frac{3}{2}$x-6,得:x=6,
则点P的坐标为(6,3);
(4)存在,如图所示: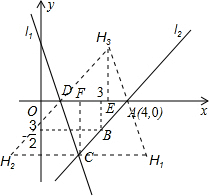
当四边形ADCH1为平行四边形时,可得CH1=AD=3,此时H1(5,-3);
当四边形ACH2D为平行四边形时,可得CH2=AD=3,此时H2(-1,-3);
当四边形ACDH3为平行四边形时,过H3作H3E⊥x轴,过C作CF⊥x轴,
∵△CFD≌△H3EA,
∴H3E=CF=3,AE=DF=1,此时H3(3,3);
综上,H的坐标为(5,-3)或(-1,-3)或(3,3).
点评 此题属于一次函数综合题,涉及的知识有:坐标与图形性质,待定系数法确定一次函数解析式,两个一次函数的交点,平行四边形的性质,熟练掌握性质是解本题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案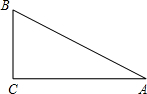 如图,在Rt△ABC中,∠C=90°,∠A=31°,AB=10,求BC的长.(结果精确到0.01)
如图,在Rt△ABC中,∠C=90°,∠A=31°,AB=10,求BC的长.(结果精确到0.01)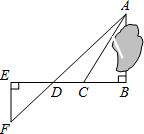 为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上,有四位同学分别测量出相关数据:甲为“BC、∠ACB”;乙为“CD、∠ACB”;丙为“EF、DE、BD”;丁为“DE、DC、BC”.根据所测数据,不能求出A、B间距离的是乙和丁同学.
为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上,有四位同学分别测量出相关数据:甲为“BC、∠ACB”;乙为“CD、∠ACB”;丙为“EF、DE、BD”;丁为“DE、DC、BC”.根据所测数据,不能求出A、B间距离的是乙和丁同学. 如图,已知∠BOD=80°,四边形ABCD的四个顶点都在圆O上,那么∠DAB的度数为140°.
如图,已知∠BOD=80°,四边形ABCD的四个顶点都在圆O上,那么∠DAB的度数为140°.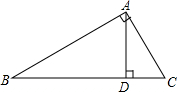 如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,则∠B=∠DAC,∠C=∠BAD.
如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,则∠B=∠DAC,∠C=∠BAD.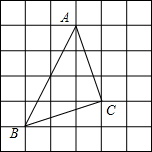 如图所示的方格纸中,每一格小正方形的边长均为1,小莉画出一个等腰直角三角形ABC,她画得对吗?请你设法验证一下,并与同伴交流各自的方法.
如图所示的方格纸中,每一格小正方形的边长均为1,小莉画出一个等腰直角三角形ABC,她画得对吗?请你设法验证一下,并与同伴交流各自的方法.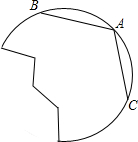 将图中的破轮子复原,已知弧上三点A,B,C.
将图中的破轮子复原,已知弧上三点A,B,C.