题目内容
4.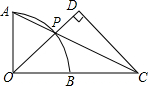 如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )
如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 过点O作OE⊥AP于点E,证△AOE∽△ACO得$\frac{AO}{AC}$=$\frac{AE}{AO}$,由OA=OB=BC=1得AC=$\sqrt{A{O}^{2}+O{C}^{2}}$=$\sqrt{5}$,从而得$\frac{1}{\sqrt{5}}$=$\frac{AE}{1}$,即AE=$\frac{\sqrt{5}}{5}$,由垂径定理得PE=AE=$\frac{\sqrt{5}}{5}$,再证△OPE∽△CPD得$\frac{PE}{PD}$=$\frac{OP}{CP}$,从而得出答案.
解答 解:过点O作OE⊥AP于点E,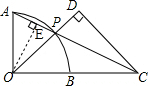
则∠AEO=∠AOC=90°,
∵∠OAE=∠CAO,
∴△AOE∽△ACO,
∴$\frac{AO}{AC}$=$\frac{AE}{AO}$,
由OA=OB=BC=1得AC=$\sqrt{A{O}^{2}+O{C}^{2}}$=$\sqrt{5}$,
则$\frac{1}{\sqrt{5}}$=$\frac{AE}{1}$,
即AE=$\frac{\sqrt{5}}{5}$,
∵OE⊥AP,
∴PE=AE=$\frac{\sqrt{5}}{5}$,
∴PC=AC-AP=$\frac{3\sqrt{5}}{5}$,
∵∠OEP=∠D=90°,∠OPE=∠CPD,
∴△OPE∽△CPD,
∴$\frac{PE}{PD}$=$\frac{OP}{CP}$,即$\frac{\frac{\sqrt{5}}{5}}{PD}$=$\frac{1}{\frac{3\sqrt{5}}{5}}$,
解得:PD=$\frac{3}{5}$.
故选:C.
点评 本题主要考查相似三角形的判定与性质、垂径定理、勾股定理等知识点,根据题意构建与直角边PD相关的相似三角形是解题的出发点也是关键.

| A. | 棱柱 | B. | 圆柱 | C. | 球 | D. | 圆锥 |
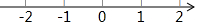 如图所示,数轴上的点A,B,C依次表示三个实数:1$\frac{1}{2}$,-1$\frac{1}{2}$,$\sqrt{3}$.
如图所示,数轴上的点A,B,C依次表示三个实数:1$\frac{1}{2}$,-1$\frac{1}{2}$,$\sqrt{3}$. 已知AB=AC,AD=AE,BA⊥AC,AD⊥AE,求证:BD=CE.
已知AB=AC,AD=AE,BA⊥AC,AD⊥AE,求证:BD=CE. 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连结DF并延长交AC于点E.若AB=8,BC=12,则线段EF的长为2.
如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连结DF并延长交AC于点E.若AB=8,BC=12,则线段EF的长为2.