题目内容
16. 已知AB=AC,AD=AE,BA⊥AC,AD⊥AE,求证:BD=CE.
已知AB=AC,AD=AE,BA⊥AC,AD⊥AE,求证:BD=CE.
分析 欲证明BD=CE,只要证明△EAC≌△DAB即可.
解答 证明:∵BA⊥AC,AD⊥AE,
∴∠EAD=∠BAC=90°,
∴∠EAC=∠DAB,
在△EAC和△DAB中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAC=∠DAB}\\{AC=AB}\end{array}\right.$,
∴△EAC≌△DAB,
∴BD=CE.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
11.设a1,a2…,a2016是从1,0,-1这三个数中取值的一列数,若a1.+a2+…+a2016=69,(a1+1)2+(a2+1)2+…+(a2016+1)2=4007,则a1,a2,…,a2016中有( )个0.
| A. | 163 | B. | 164 | C. | 165 | D. | 166 |
4.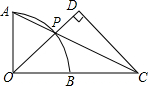 如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )
如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )
 如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )
如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
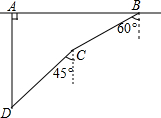 如图,一次军事演习中,蓝方在-条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截.红方行驶2000米到达C后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同距离,刚好在D处成功拦截蓝方.
如图,一次军事演习中,蓝方在-条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截.红方行驶2000米到达C后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同距离,刚好在D处成功拦截蓝方.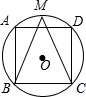 如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$中点,连接BM,CM
如图,正方形ABCD内接于⊙O,M为$\widehat{AD}$中点,连接BM,CM 如图,∠1=70°,∠2=70°.说明:AB∥CD.
如图,∠1=70°,∠2=70°.说明:AB∥CD.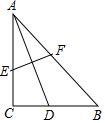 如图,在Rt△ABC中,∠C=90°,AC=BC,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,则$\frac{CE}{AE}$=$\frac{3}{5}$.
如图,在Rt△ABC中,∠C=90°,AC=BC,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,则$\frac{CE}{AE}$=$\frac{3}{5}$.