题目内容
16. 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连结DF并延长交AC于点E.若AB=8,BC=12,则线段EF的长为2.
如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连结DF并延长交AC于点E.若AB=8,BC=12,则线段EF的长为2.
分析 根据直角三角形斜边上中线是斜边的一半可得DF=$\frac{1}{2}$AB=AD=BD=4且∠ABF=∠BFD,结合角平分线可得∠CBF=∠DFB,即DE∥BC,进而可得DE=6,由EF=DE-DF可得答案.
解答 解:∵AF⊥BF,
∴∠AFB=90°,
∵AB=8,D为AB中点,
∴DF=$\frac{1}{2}$AB=AD=BD=4,
∴∠ABF=∠BFD,
又∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠CBF=∠DFB,
∴DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{CB}$=$\frac{AD}{AB}$,即$\frac{DE}{12}=\frac{4}{8}$,
解得:DE=6,
∴EF=DE-DF=2,
故答案为:2.
点评 本题主要考查直角三角形的性质和相似三角形的判定与性质,熟练运用其判定与性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.设a1,a2…,a2016是从1,0,-1这三个数中取值的一列数,若a1.+a2+…+a2016=69,(a1+1)2+(a2+1)2+…+(a2016+1)2=4007,则a1,a2,…,a2016中有( )个0.
| A. | 163 | B. | 164 | C. | 165 | D. | 166 |
4.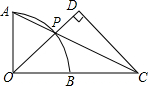 如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )
如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )
 如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )
如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
6.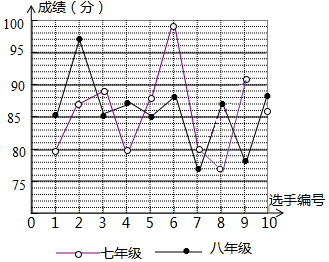 在“创建全国文明城市”演讲比赛中,学校根据初赛成绩在七、八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:
在“创建全国文明城市”演讲比赛中,学校根据初赛成绩在七、八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:
根据如图和表提供的信息,解答下列问题:
(1)请你把上边的表格填写完整;
(2)考虑平均数与方差,你认为八年级的团体成绩更好些;
(3)假设在每个年级的决赛选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些?请说明理由.
 在“创建全国文明城市”演讲比赛中,学校根据初赛成绩在七、八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:
在“创建全国文明城市”演讲比赛中,学校根据初赛成绩在七、八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:| 团体成绩 | 众数 | 平均数 | 方差 |
| 七年级 | 80 | 85.7 | 39.6 |
| 八年级 | 85 | 85.7 | 27.81 |
(1)请你把上边的表格填写完整;
(2)考虑平均数与方差,你认为八年级的团体成绩更好些;
(3)假设在每个年级的决赛选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些?请说明理由.
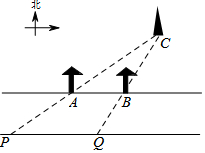 如图,一条东西走向的笔直公路,点A、B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路PQ南侧直线行走,当他到达点P的位置时,观察树A恰好挡住电视塔,即点P、A、C在一条直线上,当他继续走180米到达点Q的位置时,以同样方法观察电视塔,观察树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧PQ的距离.
如图,一条东西走向的笔直公路,点A、B表示公路北侧间隔150米的两棵树所在的位置,点C表示电视塔所在的位置.小王在公路PQ南侧直线行走,当他到达点P的位置时,观察树A恰好挡住电视塔,即点P、A、C在一条直线上,当他继续走180米到达点Q的位置时,以同样方法观察电视塔,观察树B也恰好挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为60米,求电视塔C到公路南侧PQ的距离.