题目内容
9.已知在△ABC中,三边长a、b、c满足a2+8b2+c2-4b(a+c)=0,试判断△ABC的形状并加以说明.分析 把原式根据完全平方公式进行因式分解,根据非负数的性质求出a、c的关系,判断即可.
解答 解:三角形是等腰三角形.
a2+8b2+c2-4b(a+c)=0,
a2+8b2+c2-4ab-4bc=0,
a2-4ab+4b2+c2-4bc+4b2=0,
(a-2b)2+(c-2b)2=0,
则a=2b,c=2b,
∴a=c,
则三角形是等腰三角形.
点评 本题考查的是因式分解的应用,掌握分组分解法、公式法因式分解的一般步骤是解题的关键.

练习册系列答案
相关题目
4.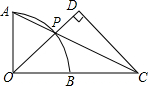 如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )
如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )
 如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )
如图,O为$\widehat{AB}$所在圆的圆心,OA⊥OB,P为$\widehat{AB}$上一点(不与点A,B重合),延长AP交OB的延长线于点C,CD⊥OP于点D.若OB=BC=1,则PD的长为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
14.已知△ABC中,AB=5,AC=7,BC=a,则a的取值范围是( )
| A. | 1<a<6 | B. | 5<a<7 | C. | 2<a<12 | D. | 10<a<14 |
 如图,∠1=70°,∠2=70°.说明:AB∥CD.
如图,∠1=70°,∠2=70°.说明:AB∥CD.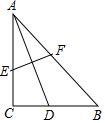 如图,在Rt△ABC中,∠C=90°,AC=BC,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,则$\frac{CE}{AE}$=$\frac{3}{5}$.
如图,在Rt△ABC中,∠C=90°,AC=BC,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,则$\frac{CE}{AE}$=$\frac{3}{5}$.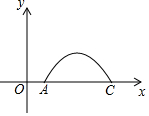 如图,一大桥有一段抛物线型的拱粱,小王骑自行车从O匀速沿直线到拱粱一端A,再匀速通过拱粱部分的桥面AC,小王从O到A用了3秒,当小王骑自行车行驶10秒时和20秒时拱粱的高度相同,则小王骑自行车通过拱粱部分的桥面AC共需24秒.
如图,一大桥有一段抛物线型的拱粱,小王骑自行车从O匀速沿直线到拱粱一端A,再匀速通过拱粱部分的桥面AC,小王从O到A用了3秒,当小王骑自行车行驶10秒时和20秒时拱粱的高度相同,则小王骑自行车通过拱粱部分的桥面AC共需24秒.