Question

如图，已知A、B两点的坐标分别为（2

3

，0）、（0，2），P是△AOB外接圆上的一点，且∠AOP=45°．
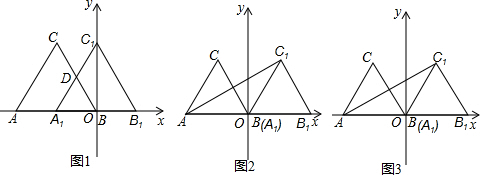
（1）如图1，求点P的坐标；
（2）如图2，连BP、AP，在PB上任取一点E，连AE，将线段AE绕A点顺时针旋转90°到AF，连BF，交AP于点G，当E在线段BP上运动时（不与B、P重合），

BE

PG

是否为定值？
（3）如图3，点Q是弧AP上一动点（不与A、P重合），连PQ、AQ、BQ，

BQ-AQ

PQ

是否为定值？若是，请求其值；若不是，求其范围．

Answer 1

考点：圆的综合题

专题：

分析：（1）作PH⊥x轴于H，连结PA、PB，由A、B两点的坐标可求出AB，由△PAB和△POH都为等腰直角三角形，得出PA=

2

2

AB=，PH=OH，设OH=t，在在Rt△PHA中，运用勾股定理求出t的值，即可得出点P的坐标．
（2）过F作FM⊥AP，由△AFM≌△EAP得出AM=PE，FM=AP=BP，再由△GFM≌△GBP得出PG=GM，利用线段关系可得出PG=

1

2

PM=

1

2

BE，故得出

BE

PG

=2是定值．
（3）作PE⊥AQ，交AQ的延长线于E，作PD⊥BQ于D，由△PBD≌△PAE，得出PD=PE，BD=AE，所以四边形PDCE为正方形，得出QD=QE，利用线段关系得出BQ-AQ=2DQ，结合△PDQ为等腰直角三角形，即可求出

BQ-AQ

PQ

=

2

是定值．

解答：解：（1）如图1，作PH⊥x轴于H，连结PA、PB，

∵∠AOB=90°，
∴AB为△AOB外接圆的直径，
∴∠BPA=90°，
∵A、B两点的坐标分别为（2

3

，0）、（0，2），
∴OA=2

3

，OB=2，
∴AB=

OA2+OB2

=4，
∵∠AOP=45°，
∴∠ABP=45°，
∴△PAB和△POH都为等腰直角三角形，
∴PA=

2

2

AB=2

2

，PH=OH，
设OH=t，则PH=t，AH=2

3

-t，
在Rt△PHA中，
∵PH²+AH²=PA²，
∴整理得t²-2

3

t+2=0，解得t₁₌

3

+1，t₂=

3

-1（舍去），
∴P点坐标为（

3

+1，

3

+1），
（2）如图2，过F作FM⊥AP，

∵∠PAE+∠MAF=90°，∠MFA+∠MAF=90°
∴∠PAE=∠MFA，
∵AE=AF，
在△AFM和△EAP，

∠EPA=∠AMF ∠PAE=∠MFA AE=AF

∴△AFM≌△EAP（AAS）
∴AM=PE，FM=AP=BP，
∴AP-AM=BP-PE，
∴PM=BE，
在△GFM和△GBP中，

∠FGM=∠PGB ∠FMB=∠BPG FM=PB

∴△GFM≌△GBP（AAS），
∴PG=GM，
∴PG=

1

2

PM=

1

2

BE，
∴

BE

PG

=2．
（3）如图3，作PE⊥AQ，交AQ的延长线于E，作PD⊥BQ于D，

∵AB为直径，
∴∠AQB=90°，
∵PD⊥BQ，PE⊥AQ，
∴四边形PDQE为矩形，
在△PBD和△PAE中，

∠BDP=∠AEP ∠PBD=∠PAE BP=AP

∴△PBD≌△PAE（AAS），
∴PD=PE，BD=AE，
∴四边形PDCE为正方形
∴QD=QE，
∴BD=AE=QE+AQ=DQ+AQ；
∴BQ-AQ=BD+DQ-AQ=DQ+AQ+DQ-AQ=2DQ，
∴

BQ-AQ

PQ

=

2DQ

PQ

，
∵∠PQB=∠PAB=45°，
∴△PDQ为等腰直角三角形，
∴PQ=

2

DQ，
∴

BQ-AQ

PQ

=

2DQ

PQ

=

2DQ

2 DQ

=

2

．

点评：此题主要考查了圆周角定理、勾股定理、等腰直角三角形的判定和性质等知识的综合应用能力；能正确作出辅助线构建出与已知和所求相关的直角三角形是解答此题的关键．