题目内容
 如图,矩形ABCD的对角线AC,BD交于点O,AC=4cm,∠AOD=120°,则BC的长为( )
如图,矩形ABCD的对角线AC,BD交于点O,AC=4cm,∠AOD=120°,则BC的长为( )A、4
| ||
| B、4cm | ||
C、2
| ||
| D、2cm |
考点:矩形的性质
专题:
分析:利用矩形对角线的性质得到OA=OB.结合∠AOD=120°知道∠AOB=60°,则△AOB是等边三角形;最后在直角△ABC中,利用勾股定理来求BC的长度即可.
解答:解:如图,∵ 矩形ABCD的对角线AC,BD交于点O,AC=4cm,
矩形ABCD的对角线AC,BD交于点O,AC=4cm,
∴OA=OB=
AC=2cm.
又∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB=2cm.
∴在直角△ABC中,∠ABC=90°,AB=2cm,AC=4m,
∴BC=
=
=2
cm.
故选:C.
 矩形ABCD的对角线AC,BD交于点O,AC=4cm,
矩形ABCD的对角线AC,BD交于点O,AC=4cm,∴OA=OB=
| 1 |
| 2 |
又∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB=2cm.
∴在直角△ABC中,∠ABC=90°,AB=2cm,AC=4m,
∴BC=
| AC2-AB2 |
| 42-22 |
| 3 |
故选:C.
点评:本题考查了矩形的性质和等边三角形的性质和判定的应用,解此题的关键是求出OA、OB的长,题目比较典型,是一道比较好的题目.

练习册系列答案
相关题目
 如图,直线AB⊥CD,垂足为O,EF是过点O的一条直线,则∠1与∠2的关系一定是( )
如图,直线AB⊥CD,垂足为O,EF是过点O的一条直线,则∠1与∠2的关系一定是( )| A、互补 | B、相等 |
| C、互余 | D、互为对顶角 |
若
是方程组
的解,则(m+n)(n-m)的值为( )
|
|
| A、16 | B、-16 | C、8 | D、-8 |
 小明同学将全校六年级学生参加课外活动人数的情况进行了统计,制成扇形统计图(如图),已知参加舞蹈类的学生有42人,则参加美术类的学生有( )
小明同学将全校六年级学生参加课外活动人数的情况进行了统计,制成扇形统计图(如图),已知参加舞蹈类的学生有42人,则参加美术类的学生有( )| A、147人 | B、63人 |
| C、60人 | D、55人 |
某商品原价269元,经连续两次降价后,售价为256元.设平均每次降价的百分率为x,则可列方程为
( )
( )
| A、269(1+x)2=256 |
| B、269(1-x)2=256 |
| C、256(1-x)2=269 |
| D、269-269x2=256 |

 在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).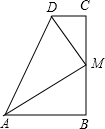 已知:如图,四边形ABCD中,AB∥CD,AM平分∠DAB,DM平分∠ADC,点M恰在BC上.
已知:如图,四边形ABCD中,AB∥CD,AM平分∠DAB,DM平分∠ADC,点M恰在BC上.