��Ŀ����
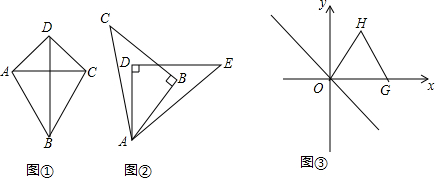
17�����ƽ���ı��Σ�����ѧϰ���Σ����壺�����ڱ߷ֱ���ȵ��ı��ν������Σ���ͼ�٣���AD=CD��AB=CB�����ı���ABCD�����Σ���1����ͬһƽ���ڣ���ABC���ADE����ͼ����ʾ���ã����С�B=��D=90�㣬AB=AD��BC��DE�ཻ�ڵ�F�������ж��ı���ABFD�Dz������Σ���˵�����ɣ�
��2��������ͼ�٣�д��һ�����ε��ж�������������⣩��
���ı���ABCD�У���AD=CD����ADB=��CDB�����ı���ABCD�����Σ�
��3����ͼ�ۣ��ڵȱ�������OGH�У���G������Ϊ��$\sqrt{3}$-1��0������ֱ��l��y=-x���Ƿ���ڵ�P��ʹ����O��G��H��PΪ������ı���Ϊ���Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���� ��1������AF��ͨ���������������ȫ��ֱ�������ε��ж�������HL���ɵó�Rt��AFB��Rt��AFD���ɴ��ҳ�BF=DF��������ζ��弴�ɵó����ۣ�
��2����Ҫ�ı���ABCD�����Σ�ֻ��֤����ABD�ա�CBD���ɣ�����ȫ�������ε��ж�������SAS�����ѡȡһ����������AD=CD����ADB=��CDB����֤����
��3������H��HP1��OG�ڵ�M��ֱ��y=-x�ڵ�P1�㣬����GP1������G��GP2��OH��N��ֱ��y=-x�ڵ�P2������HP2���ɵȱ������ε����ߺ�һ�ɵ�֪��HMΪOG�Ĵ�ֱƽ���ߣ�GNΪOH�Ĵ�ֱƽ���ߡ����ɴ˼��ó����ı���OHGP1Ϊ���Σ��ı���OGHP2Ϊ���Ρ����ٸ��ݸ��������ҳ���M��N��H������꣬���ô���ϵ�������ɵó�ֱ��HM��ֱ��GN�Ľ���ʽ���������ֱ�ߵĽ���֪ʶ�����P�����꣮
��� �⣺��1���ı���ABFD�����Σ�
���ɣ���ͼ�ڣ�����AF��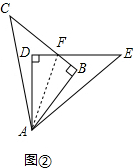
��Rt��AFB��Rt��AFD��$\left\{\begin{array}{l}{AF=AF}\\{AB=AD}\end{array}\right.$��
��Rt��AFB��Rt��AFD��HL����
��BF=DF��
�֡�AB=AD��
���ı���ABFD�����Σ�
��2����Ҫ�ı���ABCD�����Σ�ֻ���ABD�ա�CBD���ɣ�
��AD=CD����ADB=��CDBʱ���ڡ�ABD�͡�CBD�У�$\left\{\begin{array}{l}{AD=CD}\\{��ADB=��CDB}\\{BD=BD}\end{array}\right.$��
���ABD�ա�CBD��SAS����
��AB=CB��
���ı���ABCD�����Σ�
�ʴ�Ϊ��AD=CD����ADB=��CDB��
��3�����ڣ��������£�
����H��HP1��OG�ڵ�M��ֱ��y=-x�ڵ�P1�㣬����GP1������G��GP2��OH��N��ֱ��y=-x�ڵ�P2������HP2����ͼ����ʾ��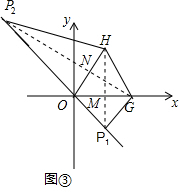
�ߡ�OGHΪ�ȱ������Σ�
��HMΪOG�Ĵ�ֱƽ���ߣ�GNΪOH�Ĵ�ֱƽ���ߣ���OG=GH=HO��
��P2O=P2H��P1O=P1G��
���ı���OHGP1Ϊ���Σ��ı���OGHP2Ϊ���Σ�
�ߡ�OGHΪ�ȱ������Σ���G������Ϊ��$\sqrt{3}$-1��0����
���H��������$\frac{\sqrt{3}-1}{2}$��$\frac{3-\sqrt{3}}{2}$������M��������$\frac{\sqrt{3}-1}{2}$��0������N��������$\frac{\sqrt{3}-1}{4}$��$\frac{3-\sqrt{3}}{4}$����
�١�H��$\frac{\sqrt{3}-1}{2}$��$\frac{3-\sqrt{3}}{2}$����M��$\frac{\sqrt{3}-1}{2}$��0����
��ֱ��HM�Ľ���ʽΪx=$\frac{\sqrt{3}-1}{2}$��
��ֱ��y=-x�е�x=$\frac{\sqrt{3}-1}{2}$����y=-$\frac{\sqrt{3}-1}{2}$��
��P1��������$\frac{\sqrt{3}-1}{2}$��-$\frac{\sqrt{3}-1}{2}$����
����ֱ��GN�Ľ���ʽΪy=kx+b�����У�
$\left\{\begin{array}{l}{0=��\sqrt{3}-1��k+b}\\{\frac{3-\sqrt{3}}{4}=\frac{\sqrt{3}-1}{4}k+b}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=\frac{3-\sqrt{3}}{3}}\end{array}\right.$��
��ֱ��GN�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+$\frac{3-\sqrt{3}}{3}$��
����$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x+\frac{3-\sqrt{3}}{3}}\\{y=-x}\end{array}\right.$����ã�$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$��
�ʵ�P2������Ϊ��-1��1����
���Ͽ�֪����ֱ��l��y=-x�ϴ��ڵ�P��ʹ����O��G��H��PΪ������ı���Ϊ���Σ���P������Ϊ��$\frac{\sqrt{3}-1}{2}$��-$\frac{\sqrt{3}-1}{2}$����-1��1����
���� ���⿼����һ�κ�����Ӧ�á����ε�Ӧ�á�ȫ�������ε��ж������ʡ�����ϵ������������ʽ�Լ����Ԫһ�η����飬����Ĺؼ��ǣ���1���ҳ�BF=DF����2��֤����ABD�ա�CBD����3���ҳ���P��λ�ã����������е��⣬��1����2���ѶȲ���3���Ѷ�Ҳ������ʵ�������У�����ͼ������������һ�������������ճ�����ϰ��Ӧʱ�����Ѻ�����ע��˼�������ȫ���ԣ�

| A�� | k��0 | B�� | k��0 | C�� | k=0 | D�� | ����ȷ�� |
 ��ͼ����Rt��ABC�У���A=90�㣬��C=60�㣬ֱ��DE��BC���ֱ�AB��AC�ڵ�D��E�����1�Ķ�����
��ͼ����Rt��ABC�У���A=90�㣬��C=60�㣬ֱ��DE��BC���ֱ�AB��AC�ڵ�D��E�����1�Ķ�����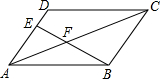 ��ͼ����?ABCD�У���E��AD���ϣ�AE=2ED������EB��AC�ڵ�F����AC=10����AFΪ4��
��ͼ����?ABCD�У���E��AD���ϣ�AE=2ED������EB��AC�ڵ�F����AC=10����AFΪ4�� ��������ij����һ����ѧʵ����У��Ծ���ֽƬ�����۵�ʵ���������������������ѧ����������̽����
��������ij����һ����ѧʵ����У��Ծ���ֽƬ�����۵�ʵ���������������������ѧ����������̽����