题目内容
如果分式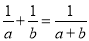 ,那么
,那么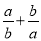 的值( )
的值( )
A. 1 B. -1 C. 2 D. -2
 B
【解析】试题分析:∵,
∴(a+b)2=ab,
即a2+b2+2ab=ab,
a2+b2=-ab,
原式====-1,
故选B.
B
【解析】试题分析:∵,
∴(a+b)2=ab,
即a2+b2+2ab=ab,
a2+b2=-ab,
原式====-1,
故选B.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图所示,已知D,E,F分别在△ABC的边BC,AB,AC上,且DE∥AF,DE=AF,将FD延长至G,使FG=2DF,连接AG,则ED,AG互相平分吗?请说明理由.
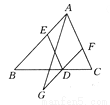
 互相平分
【解析】试题分析:求ED与AG互相平分,只要证明四边形AEGD是平行四边形即可解答,由DE∥AC,DE=AF,可得四边形AEDF是平行四边形,所以,AE∥DF且AE=DF,又FG=2DF,则AE=GD,所以,四边形AEGD是平行四边形,即可得出ED与AG互相平分.
试题解析:证明:如图,连接AD,GE,∵DE∥AC,DE=AF,∴四边形AEDF是平行四边形,∴AE∥DF且AE...
互相平分
【解析】试题分析:求ED与AG互相平分,只要证明四边形AEGD是平行四边形即可解答,由DE∥AC,DE=AF,可得四边形AEDF是平行四边形,所以,AE∥DF且AE=DF,又FG=2DF,则AE=GD,所以,四边形AEGD是平行四边形,即可得出ED与AG互相平分.
试题解析:证明:如图,连接AD,GE,∵DE∥AC,DE=AF,∴四边形AEDF是平行四边形,∴AE∥DF且AE... 如图所示,已知六边形ABCDEF中,∠A=∠B=∠C=∠D=∠E=∠F=120°.试说明AB+BC=EF+ED.
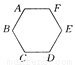
 见解析
【解析】分析:分别延长AB、DC相交于点M,延长AF、DE相交于点N,通过作辅助线我们可以得到∠MBC=∠MCB=60°,再结合三角形内角和定理即可判断△BMC是等边三角形,同理还可以得出△EFN是等边三角形;由“两组对角分别相等的四边形是平行四边形”可知四边形AMDN是平行四边形,从而可以得到AM=DN即可得出结果.
本题解析:分别延长AB、DC相交于点M,延长AF、DE相交...
见解析
【解析】分析:分别延长AB、DC相交于点M,延长AF、DE相交于点N,通过作辅助线我们可以得到∠MBC=∠MCB=60°,再结合三角形内角和定理即可判断△BMC是等边三角形,同理还可以得出△EFN是等边三角形;由“两组对角分别相等的四边形是平行四边形”可知四边形AMDN是平行四边形,从而可以得到AM=DN即可得出结果.
本题解析:分别延长AB、DC相交于点M,延长AF、DE相交... 下列命题中,其逆命题为真命题的是( )
A. 若a=b,则a2=b2 B. 同位角相等
C. 两边和一角对应相等的两个三角形全等 D. 等腰三角形两底角不相等
 C
【解析】根据互为逆命题的关系,题设和结论互换,可知:
若a=b,则a2=b2的逆命题为:若a2=b2,则a=b,是假命题;
同位角相等的逆命题为:相等的角是同位角,是假命题;
两边和一角对应相等的两个三角形全等的逆命题是:全等三角形的对应边相等,对应角相等,是真命题;
等腰三角形的两底角不相等的逆命题为:两个角不相等的三角形是等腰三角形,是假命题.
故选:C...
C
【解析】根据互为逆命题的关系,题设和结论互换,可知:
若a=b,则a2=b2的逆命题为:若a2=b2,则a=b,是假命题;
同位角相等的逆命题为:相等的角是同位角,是假命题;
两边和一角对应相等的两个三角形全等的逆命题是:全等三角形的对应边相等,对应角相等,是真命题;
等腰三角形的两底角不相等的逆命题为:两个角不相等的三角形是等腰三角形,是假命题.
故选:C... 已知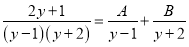 ,求A、B的值.
,求A、B的值.
 A=1,B=1.
【解析】试题分析:已知等式右边两项通分并利用同分母分式的加法法则计算,利用分式相等的条件即可求出A与B.
试题解析:
【解析】
===,
∴,
解得: .
A=1,B=1.
【解析】试题分析:已知等式右边两项通分并利用同分母分式的加法法则计算,利用分式相等的条件即可求出A与B.
试题解析:
【解析】
===,
∴,
解得: . 计算: 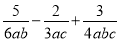 = .
= .
 【解析】试题分析:原式=
=.
故答案为: .
【解析】试题分析:原式=
=.
故答案为: . 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
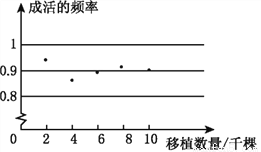
(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
 (1)0.9附近,0.9;(2)①4.5,15万棵.
【解析】(1)由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9;
(2)①5×成活率即为所求的成活的树苗棵树;
②方法1:利用成活率求得需要树苗棵树,减去已移植树苗数即为所求的树苗的棵树;
方法2:设还需移植这种树苗万棵,根据成活率及成活总数列出方程即可。
(1)0.9附近,0.9;(2)①4.5,15万棵.
【解析】(1)由图可知,成活概率在0.9上下波动,故可估计这种树苗成活的频率稳定在0.9,成活的概率估计值为0.9;
(2)①5×成活率即为所求的成活的树苗棵树;
②方法1:利用成活率求得需要树苗棵树,减去已移植树苗数即为所求的树苗的棵树;
方法2:设还需移植这种树苗万棵,根据成活率及成活总数列出方程即可。 下列命题中,其逆命题成立的是__.(只填写序号)
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
 ①④
【解析】把一个命题的条件和结论互换就得到它的逆命题,再分析逆命题是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案。
①两直线平行,同旁内角互补,正确;
②如果两个角相等,那么它们是直角,错误;
③如果两个实数的平方相等,那么这两个实数相等,错误;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形,正确.
...
①④
【解析】把一个命题的条件和结论互换就得到它的逆命题,再分析逆命题是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案。
①两直线平行,同旁内角互补,正确;
②如果两个角相等,那么它们是直角,错误;
③如果两个实数的平方相等,那么这两个实数相等,错误;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形,正确.
... 下列条形中的能代圆形图所表示的数据( )

A. 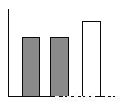 B.
B. 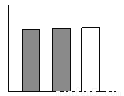 C.
C. 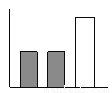 D.
D. 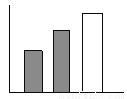
 C
【解析】由图知,阴影部分与空白部分面积相等,在给出的四个选项中,只有C中有阴影的两个矩形面积之和等于空白矩形面积.
故选C.
C
【解析】由图知,阴影部分与空白部分面积相等,在给出的四个选项中,只有C中有阴影的两个矩形面积之和等于空白矩形面积.
故选C. 
