题目内容
16.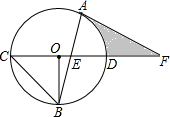 如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.
如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.(1)判断AF和⊙O的位置关系并说明理由
(2)若∠ABC=60°,BC=1cm,求阴影部分的面积.(结果保留根号)
分析 (1)连结OA,如图,由AF=AE得∠FAE=∠FEA,再利用对顶角相等和∠OBA=∠OAB可得∠OAB+∠FEA=90°,即∠OAF=90°,则OA⊥AF,然后根据切线的判定定理可判断AF为⊙O的切线;
(2)先判断△OBC为等腰直角三角形得到OB=$\frac{\sqrt{2}}{2}$BC=$\frac{\sqrt{2}}{2}$,再利用圆周角定理得到∠AOC=2∠ABC=120°,则∠AOF=180°-∠AOC=60°,接着根据正切定义计算AF=$\frac{\sqrt{6}}{2}$,然后根据三角形面积公式和扇形面积公式,利用S阴影部分=S△OAF-S扇形AOD进行计算.
解答 解:(1)AF和⊙O相切.理由如下:
连结OA,如图,
∵AF=AE,
∴∠FAE=∠FEA,
∵∠FEA=∠OEB,
∴∠FAE=∠OEB,
∵OB⊥CD,
∴∠BOE=90°,
∴∠OBE+∠OEB=90°,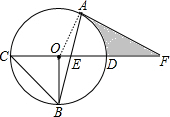
而OB=OA,
∴∠OBA=∠OAB,
∴∠OAB+∠FEA=90°,即∠OAF=90°,
∴OA⊥AF,
∴AF为⊙O的切线;
(2)∵OB⊥CD,
而OB=OC,
∴△OBC为等腰直角三角形,
∴OB=$\frac{\sqrt{2}}{2}$BC=$\frac{\sqrt{2}}{2}$,
∵∠AOC=2∠ABC=2×60°=120°,
∴∠AOF=180°-∠AOC=60°,
在Rt△OAF中,∵tan∠AOF=$\frac{AF}{AO}$,
∴AF=$\frac{\sqrt{2}}{2}$×$\sqrt{3}$=$\frac{\sqrt{6}}{2}$,
∴S阴影部分=S△OAF-S扇形AOD
=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{6}}{2}$-$\frac{60•π•(\frac{\sqrt{2}}{2})^{2}}{360}$
=$\frac{3\sqrt{3}-π}{12}$(cm2).
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了扇形面积的计算.

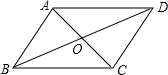 如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OA的取值范围是( )
如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OA的取值范围是( )| A. | 1cm<OA<4cm | B. | 2cm<OA<8cm | C. | 2cm<OA<5cm | D. | 3cm<OA<8cm |
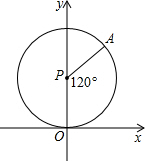 如图,⊙P与x轴切于点O,点P(0,1)在y轴上,点A在⊙P上,并且在第一象限,∠APO=120°.⊙P沿x轴正方向滚动,当点A第一次落在x轴上时为点A′,则点A′的坐标为($\frac{2π}{3}$,0)(结果保留π).
如图,⊙P与x轴切于点O,点P(0,1)在y轴上,点A在⊙P上,并且在第一象限,∠APO=120°.⊙P沿x轴正方向滚动,当点A第一次落在x轴上时为点A′,则点A′的坐标为($\frac{2π}{3}$,0)(结果保留π).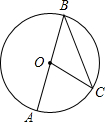 如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B=40°.
如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B=40°.