题目内容
11.把方程x2-4x+3=0写成x2-4x+4-4+3=0的形式,即(x-2)2-1=0.因式分解,得(x-2+1)(x-2-1)=0.即(x-1)(x-3)=0.发现:(-1)+(-3)=-4,(-1)×(-3)=3.结论:方程x2-(p+q)x+pq=0,可变形为(x-p)•(x-q)=0.应用上面总结的解题方法解下列方程:
(1)x2+5x+6=0;
(2)x2-7x+10=0.
分析 (1)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)先分解因式,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)x2+5x+6=0,
(x+2)(x+3)=0,
x+2=0,x+3=0,
x1=-2,x2=-3;
(2)x2-7x+10=0,
(x-2)(x-5)=0,
x-2=0,x-5=0,
x1=2,x2=5.
点评 本题考查了解一元二次方程的应用,解此题的关键是能把一元二次方程转化成一元一次方程,难度适中.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
3.下列运算正确的是( )
| A. | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{5}$ | B. | b2•b3=b6 | C. | 4a-9a=-5 | D. | (ab2)2=a2b4 |
20.-7的绝对值为( )
| A. | 7 | B. | $\frac{1}{7}$ | C. | -$\frac{1}{7}$ | D. | -7 |
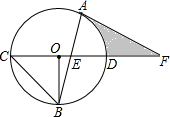 如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.
如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.