题目内容
6.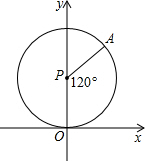 如图,⊙P与x轴切于点O,点P(0,1)在y轴上,点A在⊙P上,并且在第一象限,∠APO=120°.⊙P沿x轴正方向滚动,当点A第一次落在x轴上时为点A′,则点A′的坐标为($\frac{2π}{3}$,0)(结果保留π).
如图,⊙P与x轴切于点O,点P(0,1)在y轴上,点A在⊙P上,并且在第一象限,∠APO=120°.⊙P沿x轴正方向滚动,当点A第一次落在x轴上时为点A′,则点A′的坐标为($\frac{2π}{3}$,0)(结果保留π).
分析 当点A第一次落在x轴上时,点A′的横坐标为OA的弧长,根据弧长公式计算即可.
解答 解:∵P(0,1),⊙P与x轴切于点O,
∴⊙P的半径=1,
∴$\widehat{OA}$的长度=$\frac{120•π•1}{180}$=$\frac{2π}{3}$,
∴A′($\frac{2π}{3}$,0),
故答案为:($\frac{2π}{3}$,0).
点评 本题主要考查了切线的性质,坐标与图形的关系,弧长公式的计算,掌握公式是解题的关键.

练习册系列答案
相关题目
16.有一个从袋子中摸球的游戏,小红根据游戏规则,作出了如图所示的树形图,则此次摸球的游戏规则是( )
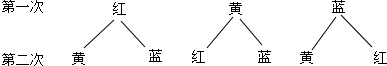
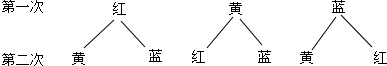
| A. | 随机摸出一个球后放回,再随机摸出1个球 | |
| B. | 随机摸出一个球后不放回,再随机摸出1个球 | |
| C. | 随机摸出一个球后放回,再随机摸出3个球 | |
| D. | 随机摸出一个球后不放回,再随机摸出3个球 |
18.方程2x=$\frac{1}{2}$的解是( )
| A. | x=-$\frac{1}{4}$ | B. | x=4 | C. | x=$\frac{1}{4}$ | D. | x=-4 |
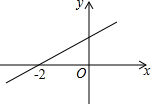 如图,一次函数y=kx+b(k>0)的图象与x轴的交点坐标为(-2,0),则关于x的不等式kx+b<0的解集是x<-2.
如图,一次函数y=kx+b(k>0)的图象与x轴的交点坐标为(-2,0),则关于x的不等式kx+b<0的解集是x<-2.
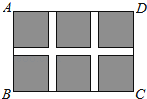 如图,某小区规划在一个长40m、宽30m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为58m2,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程(40-2x)(30-x)=6×58.
如图,某小区规划在一个长40m、宽30m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为58m2,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程(40-2x)(30-x)=6×58.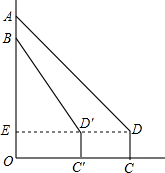 星期天,小华到小明家邀请小明到新华书店看书,当小华到达CD(点D是小华的眼睛)处时,发现小明在七楼A处,此时测得仰角为45°,继续向前走了10m到达C′D′处,发现小明在六楼B处,此时测得仰角为60°,已知楼层高AB=2.7m,求OC′的长.(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
星期天,小华到小明家邀请小明到新华书店看书,当小华到达CD(点D是小华的眼睛)处时,发现小明在七楼A处,此时测得仰角为45°,继续向前走了10m到达C′D′处,发现小明在六楼B处,此时测得仰角为60°,已知楼层高AB=2.7m,求OC′的长.(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)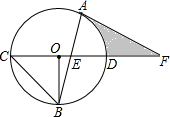 如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.
如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.