题目内容
17.某商店经营一种小商品,进价为每件20元,据市场分析,在一个月内,售价定为25元时,可卖出105件;经测算,售价每上涨1元,就少卖5件.而售价每下降1元,就多卖7件.(1)当售价定为30元时,一个月可获利多少元?
(2)当售价定为每件多少元时,一个月的获利最大?最大利润是多少元?
分析 (1)当售价定为30元时,可知每一件赚10元钱,再有售价定为25元时,可卖出105件,而售价每上涨1元,就少卖5件.可计算出一个月可获利多少元;
(2)设售价为每件x元时,一个月的获利为y元,得到y与x的二次函数关系式求出函数的最大值即可.
解答 解:(1)获利:(30-20)[105-5(30-25)]=800;
答:当售价定为30元时,一个月可获利800元;
(2)设售价为每件x元时,一个月的获利为y元,
①当售价每上涨1元,就少卖5件,由题意,得y=(x-20)[105-5(x-25)]=-5x2+330x-4600=-5(x-33)2+845,
当x=33时,y的最大值为845,
②售价每下降1元,就多卖7件,由题意,得y=(x-20)[105+7(25-x)]=-7x2+420x-5600=-7(x-30)2+700,
∵x=30>25,不符合题意,
故当售价定为33元时,一个月的利润最大,最大利润是845元.
点评 本题主要考查了二次函数的应用,能正确表示出月销售量是解题的关键.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列命题是真命题的是( )
| A. | 若直线y=-kx-2过第一、三、四象限,则k<0 | |
| B. | 三角形三条角平分线的交点到三个顶点的距离相等 | |
| C. | 如果∠A=∠B,那么∠A和∠B是对顶角 | |
| D. | 如果a•b=0,那么a=0 |
2. 如图:已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列三角形中与△BDF一定相似的是( )
如图:已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列三角形中与△BDF一定相似的是( )
 如图:已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列三角形中与△BDF一定相似的是( )
如图:已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列三角形中与△BDF一定相似的是( )| A. | △BAC | B. | △BEC | C. | △BAE | D. | △BFA |
 如图,已知在△ABC中,AD是BC边的中线,AE=EF=CF,BE与AD交于点G,求DF:GB的值.
如图,已知在△ABC中,AD是BC边的中线,AE=EF=CF,BE与AD交于点G,求DF:GB的值.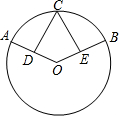 如图,在⊙O中,点C是$\widehat{AB}$的中点,D、E分别是半径OA和OB的中点,求证:CD=CE.
如图,在⊙O中,点C是$\widehat{AB}$的中点,D、E分别是半径OA和OB的中点,求证:CD=CE.