题目内容
5.圆的一条弦恰好为半径长,这条弦所对的圆周角为30或150度.分析 根据题意画出相应的图形,如图所示,由半径等于弦长,得到三角形AOB为等边三角形,利用等边三角形的性质得到∠AOB为60°,利用同弧所对的圆心角等于所对圆周角的2倍求出∠ACB的度数,再利用圆内接四边形的对角1互补求出∠ADB的度数,即可得出弦AB所对圆周角的度数.
解答 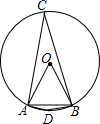 解:根据题意画出相应的图形,如图所示,
解:根据题意画出相应的图形,如图所示,
∵OA=OB=AB,
∴△AOB为等边三角形,
∴∠AOB=60°,
∵∠AOB与∠ACB都对$\widehat{AB}$,
∴∠ACB=$\frac{1}{2}$∠AOB=30°,
又四边形ACBD为圆O的内接四边形,
∴∠ACB+∠ADB=180°,
∴∠ADB=150°,
则弦AB所对的圆周角为30°或150°.
故答案为:30或150.
点评 此题考查了圆周角定理,等边三角形的性质,以及圆内接四边形的性质,熟练掌握圆周角定理是解本题的关键.

练习册系列答案
相关题目
10.下列表述中,能确定准确位置的是( )
| A. | 教室第三排 | B. | 湖南东路 | ||
| C. | 南偏东40° | D. | 东经112°,北纬51° |
14.代数式 0,3-a,$\frac{1+a}{4}$,$\frac{1}{3}{a^2}{b^2}(c-1)$,6(x2+y2),-3x+6y,a,π+1中,单项式个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15. 2015年元旦前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
2015年元旦前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)若用w(元)表示工艺厂试销该工艺品每天获得的利润,试求w(元)与x(元)之间的函数关系式.
(3)若该工艺品的每天的总成本不能超过2500元,那么销售单价定为多少时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?
 2015年元旦前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
2015年元旦前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)若用w(元)表示工艺厂试销该工艺品每天获得的利润,试求w(元)与x(元)之间的函数关系式.
(3)若该工艺品的每天的总成本不能超过2500元,那么销售单价定为多少时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?