题目内容
10.某风景区门票价格规定如下表:| 购票人数 | 1-50人 | 51-100人 | 100人以上 |
| 每人门票价 | 26元 | 22元 | 18元 |
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可省多少元?
分析 (1)先用2556÷108=23$\frac{2}{3}$,26>23$\frac{2}{3}$>22元,从而可知甲班级多于50人,乙班人数少于50人.设甲班x人,乙班(108-x)人,根据一共2556元列方程求解即可;
(2)求得联合购买的票价,然后减去单独购买的票价即可.
解答 解:(1)2556÷108=23$\frac{2}{3}$,
∵26>23$\frac{2}{3}$>22元,
∴甲班级多于50人,乙班人数少于50人.
设甲班x人,乙班(108-x)人.
根据题意得:22x+26(108-x)=2556.
解得:x=63.
108-63=45(人).
答:甲班有63人,乙班有45人.
(2)2556-108×18=612(元).
答:作为一个团体购票,可省612元.
点评 本题主要考查的是一元一次方程的应用,确定出甲乙两班人数的范围并根据票价总额为2556元列出方程是解题的关键.

练习册系列答案
相关题目
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到AB的距离是( )
| A. | $\frac{12}{5}$ | B. | $\frac{4}{25}$ | C. | $\frac{3}{4}$ | D. | $\frac{9}{4}$ |
 如图,点C在线段AB上,D是线段AC的中点,若BD=5cm,BC=2cm,则AB的长度为8cm.
如图,点C在线段AB上,D是线段AC的中点,若BD=5cm,BC=2cm,则AB的长度为8cm.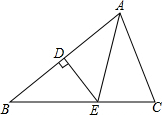 已知,如图,∠ABC中,AB=BC,DE是AB的中垂线,且BE=AC,求证:∠B=∠EAC.
已知,如图,∠ABC中,AB=BC,DE是AB的中垂线,且BE=AC,求证:∠B=∠EAC.