Question

10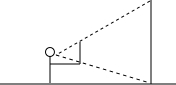．如图，某位同学拿着一把有刻度的尺子，站在距电线杆30m的位置，把手臂向前伸直，将尺子竖直，看到尺子遮住电线杆时的刻度为12cm，已知手臂长为60cm，求电线杆的高度．

Answer 1

分析 如图，FB=30m，CD=12cm=0.12m，DE=60cm=0.6m作OH⊥AB于H，交CD于M，易得OM=ED=0.6m，OH=FB=30m，再证明△OCD∽△OAB，然后利用相似比可计算出AB，从而得到电线杆的高度．

解答 解：如图，FB=30m，CD=12cm=0.12m，DE=60cm=0.6m
作OH⊥AB于H，交CD于M，则OM=ED=0.6m，OH=FB=30m，
∵CD∥AB，
∴△OCD∽△OAB，
∴$\frac{CD}{AB}$=$\frac{OM}{OH}$，即$\frac{0.12}{AB}$=$\frac{0.6}{30}$，解得AB=6（m）．
答：电线杆的高度为6m．

点评 本题考查了相似三角形的应用：利用影长测量物体的高度；利用相似测量河的宽度；借助标杆或直尺测量物体的高度．找出几何图形上相应线段的长是解题的关键．