题目内容
18．解不等式组：$\left\{\begin{array}{l}{2x+3≥3（x+2）}\\{\frac{x+3}{3}＞\frac{x-1}{5}+\frac{2}{3}}\end{array}\right.$．分析 先解不等式组，分别求出x的取值范围，然后画出数轴，数轴上相交的点的集合就是该不等式的解集．若没有交点，则不等式无解．
解答 解：不等式可化为：$\left\{\begin{array}{l}{x≤-3}\\{x＞-4}\end{array}\right.$，
在数轴上可表示为：
∴不等式组的解集为：-4＜x≤-3．
点评 本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
相关题目
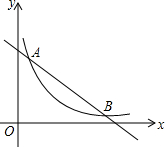如图，在平面直角坐标系中，A，B两点的纵坐标分别为7和1，直线AB与y轴所夹锐角为60°．
如图，AO=CO，DO=BO，∠COA=∠DOB，求证：△AOB≌△COD．
如图，每个小正方形的边长都为1，则以A，B，C，D，E，F中的三点为顶点且面积为1的三角形共有6个．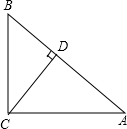
已知在△ABC中，∠ACB=90°，CD⊥AB，AC=3$\sqrt{10}$，BD=9，则AD的长为6，CD的长为3$\sqrt{6}$，BC的长为3$\sqrt{15}$．
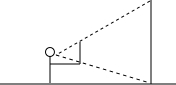如图，某位同学拿着一把有刻度的尺子，站在距电线杆30m的位置，把手臂向前伸直，将尺子竖直，看到尺子遮住电线杆时的刻度为12cm，已知手臂长为60cm，求电线杆的高度．
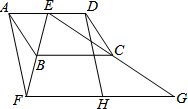如图，四边形ABCD为平行四边形，E为AD上的一点，连接EB并延长，使BF=BE，连接EC并延长，使CG=CE，连接FG．H为FG的中点，连接DH．