题目内容
1.李明同学喜欢自行车和长跑两项运动,每周进行两次训练,每次训练骑自行车的平均速度和跑步的平均速度都分别相同,且骑自行车的平均速度是跑步的平均速度的3倍,第一次训练时,他骑自行车骑了一段路程接着又跑步3000米,跑步的时间比骑自行车的时间多10分钟,设他跑步的速度为x米/分.(1)用含x的代数式表示第一次训练时他骑自行车的路程;
(2)第二次训练时,他将第一次训练中跑步的路程段改为骑自行车,骑自行车的路程段改为跑步,则全程共需要20分钟,试求他每次训练的总路程.
分析 (1)先根据时间=路程÷速度,求出跑步的时间,进一步表示出骑自行车的时间,再根据路程=速度×时间,路程算式求得第一次训练时他骑自行车的路程;
(2)根据等量关系:第二次训练时,全程共需要20分钟,列出方程求解即可.
解答 解:(1)第一次训练时跑步的时间为$\frac{3000}{x}$分,
第一次训练时骑自行车的时间为$\frac{3000}{x}$-10分,
第一次训练时他骑自行车的路程为3x×($\frac{3000}{x}$-10)=9000-30x米;
(2)依题意有:
$\frac{3000}{3x}$+$\frac{9000-30x}{x}$=20,
解得x=200,
3000+9000-30x
=3000+9000-6000
=6000.
答:他每次训练的总路程是6000米.
点评 本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.利用分式方程解应用题时,一般题目中会有两个相等关系,这时要根据题目所要解决的问题,选择其中的一个相等关系作为列方程的依据,而另一个则用来设未知数.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 把小圆形场地的半径增加5m得到大圆形场地,场地面积增加了一倍,求小圆形场地的半径.
把小圆形场地的半径增加5m得到大圆形场地,场地面积增加了一倍,求小圆形场地的半径. 如图,AO=CO,DO=BO,∠COA=∠DOB,求证:△AOB≌△COD.
如图,AO=CO,DO=BO,∠COA=∠DOB,求证:△AOB≌△COD. 小红家九月份的生活用水情况如图所示,小红的妈妈说:“洗衣用水约为2.6立方米.”请你估计小红家一年的总用水量?
小红家九月份的生活用水情况如图所示,小红的妈妈说:“洗衣用水约为2.6立方米.”请你估计小红家一年的总用水量? 如图,每个小正方形的边长都为1,则以A,B,C,D,E,F中的三点为顶点且面积为1的三角形共有6个.
如图,每个小正方形的边长都为1,则以A,B,C,D,E,F中的三点为顶点且面积为1的三角形共有6个.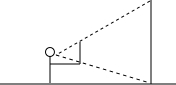 如图,某位同学拿着一把有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子遮住电线杆时的刻度为12cm,已知手臂长为60cm,求电线杆的高度.
如图,某位同学拿着一把有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子遮住电线杆时的刻度为12cm,已知手臂长为60cm,求电线杆的高度.