题目内容
14.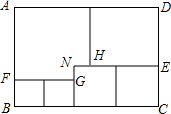 如图,用三种大小不同的五个正方形和一个缺角的长方形拼成长方形ABCD,其中,NH=NG=1cm,设BF=acm.
如图,用三种大小不同的五个正方形和一个缺角的长方形拼成长方形ABCD,其中,NH=NG=1cm,设BF=acm.(1)用含a的代数式表示CE=1+acm,DE=2a+1cm;
(2)求长方形ABCD的周长.(用含a的代数式表示)
分析 (1)根据正方形的性质和线段的和差关系即可得出CE和DE;
(2)先求出长方形ABCD的长和宽,再求得2(长+宽)即可得出长方形ABCD的周长.
解答 解:(1)∵BF=acm,NH=NG=1cm,
∴CE=BF+NG=a+1,
∴NE=2CE=2a+2,
∴EH=2a+2-1=2a+1,
∴DE=EH=2a+1;
故答案为1+a,2a+1;
(2)∵BC=FG+EN=2a+2a+2=4a+2,CD=CE+DE=1+a+2a+1=3a+2,
∴长方形ABCD的周长=2(4a+2+3a+2)=14a+8.
点评 此题考查了列代数式,主要是能够用不同的方法表示同一个长方形的宽,注意各个正方形的边长之间的数量关系.

练习册系列答案
相关题目
4.已知$\sqrt{(a-2)^{2}}$+$\sqrt{(a-1)^{2}}$=2a-3,则( )
| A. | 1<a<2 | B. | a≥2 | C. | a≤1 | D. | 1≤a≤2 |
6.下表中是一次函数的自变量x与函数y的部分对应值.
求:(1)一次函数的解析式;(2)求p的值.
| x | -2 | 0 | 1 |
| y | 3 | P | 0 |
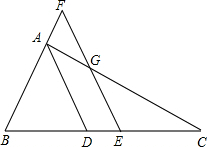 如图,AD为△ABC的平分线,E为BC的中点,EF∥AD交BA的延长线于F,交AC于G.
如图,AD为△ABC的平分线,E为BC的中点,EF∥AD交BA的延长线于F,交AC于G.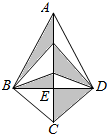 在四边形ABCD中,AC⊥BD于E,且BE=DE,已知AC=10,BD=5,则图中阴影部分的面积=12.5.
在四边形ABCD中,AC⊥BD于E,且BE=DE,已知AC=10,BD=5,则图中阴影部分的面积=12.5.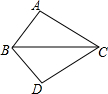 如图所示,把△ABC沿直线BC翻折180°到△DBC,那么△ABC和△DBC是全等图形(填“是”或“不是”);若△ABC的面积为2,那么△BDC的面积为2.
如图所示,把△ABC沿直线BC翻折180°到△DBC,那么△ABC和△DBC是全等图形(填“是”或“不是”);若△ABC的面积为2,那么△BDC的面积为2.