题目内容
2.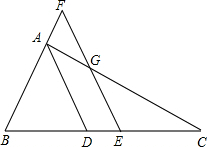 如图,AD为△ABC的平分线,E为BC的中点,EF∥AD交BA的延长线于F,交AC于G.
如图,AD为△ABC的平分线,E为BC的中点,EF∥AD交BA的延长线于F,交AC于G.(1)求证:AF=AG;
(2)求证:BF=CG;
(3)求$\frac{AB+AC}{CG}$的值.
分析 (1)由角平分线的定义可知∠1=∠2,由平行线的性质可知∠F=∠1,∠2=∠3,故此∠F=∠3,由等角对等边可知AF=AG;
(2)延长FE到H使FE=EH.先证明△BFE≌△CHE,从而得到∠H=∠F,BF=CH,由∠H=∠4,可知HC=CG,故此BF=CG;
(3)根据AB+AC=AB+AG+CG=AB+AF+CG=BF+GC,可知AB+AC=2GC.
解答 解:(1)如图1所示:
∵AD平分∠BAC,
∴∠1=∠2.
∵AD∥EF,
∴∠F=∠1,∠2=∠3.
∴∠F=∠3.
∴AF=AG.
(2)如图2,延长FE到H使FE=EH.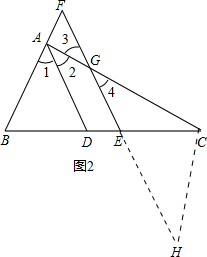
在△BFE和△CHE中,
$\left\{\begin{array}{l}{EF=EH}\\{∠FEB=∠HEC}\\{BE=CE}\end{array}\right.$,
∴△BFE≌△CHE.
∴∠H=∠F,BF=CH.
又∵∠F=∠3=∠4,
∴∠H=∠4.
∴HC=CG.
∴BF=CG.
(3)$\frac{AB+AC}{CG}$=$\frac{AB+AG+GC}{GC}$=$\frac{AB+AF+GC}{GC}$=$\frac{BF+GC}{GC}$=$\frac{2GC}{GC}$=2.
点评 本题主要考查的是全等三角形的性质和判定、等腰三角形的性质和判定,掌握本题的辅助线的作法是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图,已知数轴上点A、B表示的数为6,-4,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A、B表示的数为6,-4,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.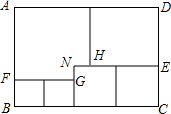 如图,用三种大小不同的五个正方形和一个缺角的长方形拼成长方形ABCD,其中,NH=NG=1cm,设BF=acm.
如图,用三种大小不同的五个正方形和一个缺角的长方形拼成长方形ABCD,其中,NH=NG=1cm,设BF=acm.