题目内容
4.先化简,再求值:[(x-2y)2+(x+2y)(x-2y)-2xy]÷2x,其中x=2,y=-$\frac{1}{2}$.分析 原式中括号中利用平方差公式,完全平方公式化简,去括号合并后利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
解答 解:原式=(x2-4xy+4y2+x2-4y2-2xy)÷2x=(2x2-6xy)÷2x=x-3y,
当x=2,y=-$\frac{1}{2}$时,原式=2+$\frac{3}{2}$=3$\frac{1}{2}$.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15. 如图,已知△ABC≌△CDA,则下列结论中,一定成立的是( )
如图,已知△ABC≌△CDA,则下列结论中,一定成立的是( )
 如图,已知△ABC≌△CDA,则下列结论中,一定成立的是( )
如图,已知△ABC≌△CDA,则下列结论中,一定成立的是( )| A. | BC=AC | B. | AD=AB | C. | CD=AC | D. | AB=CD |
9.判断下列各组线段中,哪组能组成三角形( )
| A. | a=2.5cm,b=3cm,c=5cm | B. | e=6.3cm,f=6.3cm,g=12.6cm | ||
| C. | m=4cm,n=6cm,p=lcm | D. | a+1,a+1,2a+2 (a>0) |
16.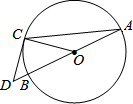 如图,AB是⊙O的直径,C、A是⊙O上的点,∠CAB=20°,过点C作⊙O的切线交AB的延长线于点D,则∠D等于( )
如图,AB是⊙O的直径,C、A是⊙O上的点,∠CAB=20°,过点C作⊙O的切线交AB的延长线于点D,则∠D等于( )
 如图,AB是⊙O的直径,C、A是⊙O上的点,∠CAB=20°,过点C作⊙O的切线交AB的延长线于点D,则∠D等于( )
如图,AB是⊙O的直径,C、A是⊙O上的点,∠CAB=20°,过点C作⊙O的切线交AB的延长线于点D,则∠D等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
13. 下列对一次函数y=2x+1的图形描述不正确的是( )
下列对一次函数y=2x+1的图形描述不正确的是( )
 下列对一次函数y=2x+1的图形描述不正确的是( )
下列对一次函数y=2x+1的图形描述不正确的是( )| A. | 图象经过一、二、三象限 | |
| B. | 图象与x轴、y轴的交点坐标分别为(-$\frac{1}{2}$,0)、(0,1) | |
| C. | y的值随着x的增大而减小 | |
| D. | 图象与坐标轴所围成的三角形面积为$\frac{1}{4}$ |
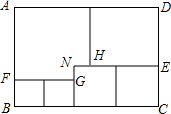 如图,用三种大小不同的五个正方形和一个缺角的长方形拼成长方形ABCD,其中,NH=NG=1cm,设BF=acm.
如图,用三种大小不同的五个正方形和一个缺角的长方形拼成长方形ABCD,其中,NH=NG=1cm,设BF=acm.