题目内容
已知抛物线y=a(x+3)2+h(a≠0)与x轴交于A(x1,0),B(-1,0)两点,则线段AB的长度为( )
| A、1 | B、4 | C、6 | D、8 |
考点:抛物线与x轴的交点
专题:
分析:易求得该抛物线的对称轴,根据抛物线与x轴交点关于对称轴对称即可求得x1的值,即可解题.
解答:解:∵抛物线解析式为y=a(x+3)2+h(a≠0),
∴对称轴为x=-3,
∵x轴交于A(x1,0),B(-1,0)两点,
∴x1=-5,
∴线段AB的长度=(-1)-(-5)=4.
故选 B.
∴对称轴为x=-3,
∵x轴交于A(x1,0),B(-1,0)两点,
∴x1=-5,
∴线段AB的长度=(-1)-(-5)=4.
故选 B.
点评:本题考查了抛物线与x轴交点关于对称轴对称的性质,本题中求得该抛物线对称轴是解题的关键.

练习册系列答案
相关题目
下列运算正确的是( )
A、
| ||
| B、5-8=-3 | ||
| C、23=6 | ||
| D、-32=9 |
如果x>y,那么下列选项正确的是( )
| A、-3x>-3y | ||||
B、
| ||||
| C、x2>y2 | ||||
| D、x-5>y-5 |
 如图,△ABC和△DCE都是等腰三角形,∠ACB=∠DCE=90°,点P、M、N分别为DE、BE、AD的中点.求证:MN=
如图,△ABC和△DCE都是等腰三角形,∠ACB=∠DCE=90°,点P、M、N分别为DE、BE、AD的中点.求证:MN=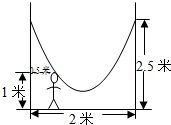 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为( )米.