题目内容
求半径为20的圆内接正三角形的边长和面积.
考点:正多边形和圆
专题:
分析:欲求△ABC的边长,把△ABC中BC边当弦,作BC的垂线,在Rt△BOD中,求BD的长;根据垂径定理知:BC=2BD,从而求正三角形的边长,再由锐角三角函数的定义求出AD的长,进而得出其面积.
解答:解:如图所示: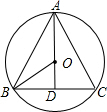
∵半径为20的圆的内接正三角形,
∴在Rt△BOD中,OB=20,∠OBD=30°,
∴BD=cos30°×OB=
×20=10
,
∵BD=CD,
∴BC=2BD=20
,
∴AD=AB•sin60°=20
×
=30,
∴S△ABC=
BC•AD=
×20
×30=300
.
故它的内接正三角形的边长为20
,面积为300
.

∵半径为20的圆的内接正三角形,
∴在Rt△BOD中,OB=20,∠OBD=30°,
∴BD=cos30°×OB=
| ||
| 2 |
| 3 |
∵BD=CD,
∴BC=2BD=20
| 3 |
∴AD=AB•sin60°=20
| 3 |
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故它的内接正三角形的边长为20
| 3 |
| 3 |
点评:本题主要考查了正多边形和圆,根据正三角形的性质得出∠OBD=30°是解题关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
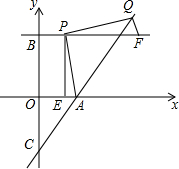 在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=Rt∠,直线AQ交y轴于点C
在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=Rt∠,直线AQ交y轴于点C