题目内容
 如图,△ABC和△DCE都是等腰三角形,∠ACB=∠DCE=90°,点P、M、N分别为DE、BE、AD的中点.求证:MN=
如图,△ABC和△DCE都是等腰三角形,∠ACB=∠DCE=90°,点P、M、N分别为DE、BE、AD的中点.求证:MN=| 2 |
考点:全等三角形的判定与性质,等腰直角三角形,三角形中位线定理
专题:证明题
分析:连接CP,NP,易证CN=EM,易证CP=EP=PD,∠E=∠D=∠PCD=45°,即可证明△EPM≌△PCN,可得PM=PN,∠EPM=∠CPN,根据∠EPM+∠MPC=90°,可证明∠MPN=90°,即可解题.
解答:证明:连接CP,NP,
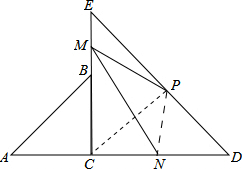
设AC=BC=a,EM=BM=b,则CE=2b+a=CD,AD=2b+2a,
∵N为AD中点,∴AN=a+b,
∵AC=a,∴CN=EM=a,
∵CP为等腰直角三角形ECD的中线,
∴CP=EP=PD,∠E=∠D=∠PCD=45°,
在△EPM和△PCN中,
,
∴△EPM≌△PCN,(SAS)
∴PM=PN,∠EPM=∠CPN,
∵∠EPM+∠MPC=90°,
∴∠CPN+∠MPC=90°,即∠MPN=90°,
∴MN2=MP2+NP2,
∴MN=
MP.

设AC=BC=a,EM=BM=b,则CE=2b+a=CD,AD=2b+2a,
∵N为AD中点,∴AN=a+b,
∵AC=a,∴CN=EM=a,
∵CP为等腰直角三角形ECD的中线,
∴CP=EP=PD,∠E=∠D=∠PCD=45°,
在△EPM和△PCN中,
|
∴△EPM≌△PCN,(SAS)
∴PM=PN,∠EPM=∠CPN,
∵∠EPM+∠MPC=90°,
∴∠CPN+∠MPC=90°,即∠MPN=90°,
∴MN2=MP2+NP2,
∴MN=
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△EPM≌△PCN是解题的关键.

练习册系列答案
相关题目
2014年“双十一”当天,阿里巴巴当天交易额达到惊人的571亿元,请用科学记数法表示571亿为( )
| A、5.71×108 |
| B、5.71×1010 |
| C、5.71×109 |
| D、5.71×1011 |
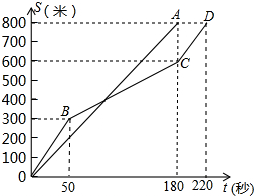 在某市初中学业水平考试体育学科800米能力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.下列说法错误的是( )
在某市初中学业水平考试体育学科800米能力测试中,某考点同时起跑的甲和乙所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD.下列说法错误的是( )| A、甲比乙先到达终点 |
| B、跑步过程中甲的速度不变 |
| C、起跑后400米内,乙始终在甲的前面 |
| D、在起跑后180米时,甲乙两人相遇 |
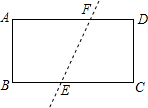 已知,如图,在矩形(两组对边平行且相等,四个内角都为直角)ABCD中,AB=4,BC=8,把它沿直线EF折叠,点C与点A重合,求CE的长.
已知,如图,在矩形(两组对边平行且相等,四个内角都为直角)ABCD中,AB=4,BC=8,把它沿直线EF折叠,点C与点A重合,求CE的长.