题目内容
已知二次函数y=a（x-1）2+m的图象与x轴交于点（-2，0），则图象与x轴的另一交点坐标是 ．
考点：抛物线与x轴的交点
专题：
分析：先根据题意得出二次函数y=a（x-1）2+m的对称轴方程，再根据两交点坐标关于对称轴对称即可得出结论．
解答：解：设图象与x轴的另一交点坐标是（a，0）．
∵二次函数的解析式为y=a（x-1）2+m，
∴其对称轴是直线x=1．
∵图象与x轴交于点（-2，0），
∴
=1，解得a=4，
∴图象与x轴的另一交点坐标是（4，0）．
故答案为：（4，0）．
∵二次函数的解析式为y=a（x-1）2+m，
∴其对称轴是直线x=1．
∵图象与x轴交于点（-2，0），
∴
| -2+a |
| 2 |
∴图象与x轴的另一交点坐标是（4，0）．
故答案为：（4，0）．
点评：本题考查的是抛物线与x轴的交点，熟知x轴上点的坐标特点是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
近似数34.2万精确到的数位是（ ）
| A、十分位 | B、十位 | C、百位 | D、千位 |
如图，将半径为3的圆形纸片，按下列顺序折叠，若
和
都经过圆心O，则阴影部分的面积是（ ）
 |
| AB |
|
| BC |
| A、π | B、2π | C、3π | D、4π |
将正整数按图所示的规律排列，若用有序数对（m，n）表示第m排从左到右第n个数，如（4，3）表示整数9，则（7，2）表示的整数是
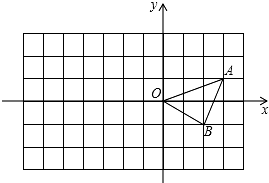如图，已知O是坐标原点，A、B的坐标分别为（3，1），（2，-1）．