题目内容
17. 已知二次函数y=ax2-2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B垂直于x轴的直线交于点D,且CP:PD=1:2
已知二次函数y=ax2-2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B垂直于x轴的直线交于点D,且CP:PD=1:2(1)求A、B两点的坐标;
(2)若tan∠PDB=1,求这个二次函数的关系式;
(3)在(2)的基础上,将直线CP先绕点C旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,Q是直线n上的动点,是否存在点Q,使△OPQ为直角三角形?若存在,求出所有点Q的坐标;若不存在,请说明理由.
分析 (1)先求得抛物线的对称轴为x=1,然后利用平行线分线段成比例定理求得OE:EB的值,从而得到点B的坐标,利用抛物线的对称性可求得点A的坐标;
(2)过点C作CF⊥PE,垂足为F.先求得点C和点P的坐标(用含字母的式子表示),然后可得到PF=a,然后利用锐角三角函数的定义可求得a的值,然后将点A和点B的坐标代入抛物线的解析式可求得c的值.;
(3)先求得抛物线的顶点坐标,然后再求得直线n=-2.设点Q的坐标为(a,-2),依据两点间的距离公式可知:PO2=17,PQ2=(1-a)2+4,OQ2=a2+4,
最后依据勾股定理的逆定理列方程求解即可.
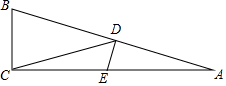
解答 解:(1)如图所示: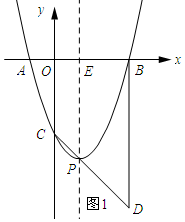
∵由题意可知:抛物线的对称轴为x=1,
∴OE=1.
∵OC∥PE∥BD,
∴$\frac{EO}{BE}=\frac{CP}{PD}$=$\frac{1}{2}$.
∴BE=2.
∴OB=3.
∴B(3,0).
∵点A与点B关于PE对称,
∴点A的坐标为(-1,0).
(2)过点C作CF⊥PE,垂足为F.
将x=0代入得:y=c,
∴点C的坐标为(0,c).
将x=1代入得y=-a+c.
∴点P的坐标为(1,-a+c).
∴PF=a.
∵PE∥BD,tan∠BPD=1,
∴tan∠FPC=1.
∴$\frac{CF}{PF}$=$\frac{1}{a}$=1,解得a=1.
将a=1代入抛物线的解析式得:y=x2-2x+c.
将点A的坐标代入得:1+2+c=0,解得:c=-3.
∴抛物线的解析式为y=x2-2x-3.
(3)∵y=x2-2x-3=(x-1)2-4,
∴点P的坐标为(1,-4).
由题意可知:直线n=-2.
设点Q的坐标为(a,-2),依据两点间的距离公式可知:PO2=17,PQ2=(1-a)2+4,OQ2=a2+4,
当PQ2+OQ2=PO2时,(1-a)2+4+a2+4=17,解得:a=$\frac{-1+\sqrt{17}}{2}$或a=$\frac{-1-\sqrt{17}}{2}$.
∴点Q的坐标为($\frac{-1+\sqrt{17}}{2}$,-2)或($\frac{-1-\sqrt{17}}{2}$,-2).
当PO2+PQ2=OQ2时,17+(1-a)2+4=a2+4,解得a=9.
∴点Q的坐标为(9,-2).
当PO2+OQ2=PQ2时,17+a2+4=(1-a)2+4,解得:a=-8.
∴点Q的坐标为(-8,-2).
综上所述,点Q的坐标为($\frac{-1+\sqrt{17}}{2}$,-2)或($\frac{-1-\sqrt{17}}{2}$,-2)或(9,-2)或(-8,-2).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了抛物线的对称性,锐角三角函数的定义,平行线分线段成比例定理,勾股定理的逆定理,作CF垂直于对称轴,利用锐角三角函数的定义求得a的值是解题的关键.

 新思维寒假作业系列答案
新思维寒假作业系列答案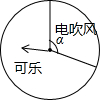 为抵制乐天,吸引顾客,某商场进行一个有奖销售的促销活动,设立了一个可以自由转动的转盘,并规定,顾客购物200元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
为抵制乐天,吸引顾客,某商场进行一个有奖销售的促销活动,设立了一个可以自由转动的转盘,并规定,顾客购物200元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 72 | 142 | 278 | 355 | b | 701 |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.72 | 0.71 | 0.695 | a | 0.705 | 0.701 |
(2)请估计当n很大时,落在“可乐”区域的频率将会接近0.7;假如你去转动该转盘一次,你获得“可乐”的概率约是0.7;(结果全部精确到0.1)
(3)在该转盘中,表示“电吹风”区域的扇形的圆心角a约是多少度?(结果精确到1°)
| 时间 | 0:00 | 4:00 | 8:00 | 12:00 | 16:00 | 20:00 |
| PM2.5(mg/m3) | 0.027 | 0.035 | 0.032 | 0.014 | 0.016 | 0.032 |
| A. | 0.032,0.0295 | B. | 0.026,0.0295 | C. | 0.026,0.032 | D. | 0.032,0.027 |
 如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E.
如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E. 在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.
在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.