题目内容
3.先化简,再求值:($\frac{x-2}{x-1}-\frac{x}{x+1}$)÷$\frac{x+2}{{x}^{2}-1}$,其中x=$\sqrt{3}-2$.分析 首先将括号里面通分运算,进而利用分式乘除运算法则计算得出答案.
解答 解:($\frac{x-2}{x-1}-\frac{x}{x+1}$)÷$\frac{x+2}{{x}^{2}-1}$,
=[$\frac{(x-2)(x+1)}{(x-1)(x+1)}$-$\frac{x(x-1)}{(x-1)(x+1)}$]×$\frac{(x-1)(x+1)}{x+2}$
=$\frac{{x}^{2}-x-2-{x}^{2}+x}{(x+1)(x-1)}$×$\frac{(x-1)(x+1)}{x+2}$
=$\frac{-2}{(x+1)(x-1)}$×$\frac{(x-1)(x+1)}{x+2}$
=-$\frac{2}{x+2}$
把x=$\sqrt{3}-2$代入上式可得:
原式=-$\frac{2}{\sqrt{3}}$=-$\frac{2\sqrt{3}}{3}$.
点评 此题主要考查了分式的化简求值,正确掌握运算法则是解题关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
10.用科学记数法表示0.009987,并保留两个有效数字是( )
| A. | 9.9×10-3 | B. | 1×10-2 | C. | 1.0×10-2 | D. | 0.10×10-3 |
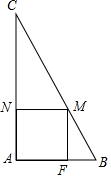 如图,在Rt△ABC中,∠A=90°,AB=2cm,AC=4cm.
如图,在Rt△ABC中,∠A=90°,AB=2cm,AC=4cm.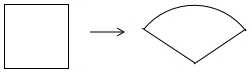 如图,某数学兴趣小组将周长为12的正方形铁丝框变形为一个扇形框,则所得扇形的面积的最大值为9.
如图,某数学兴趣小组将周长为12的正方形铁丝框变形为一个扇形框,则所得扇形的面积的最大值为9.