题目内容
如图，AB为⊙O的直径，点C在⊙O 上，点P是直径AB上的一点，（不与A，B重合），过点P作AB的垂线交BC的延长线于点Q．（1）点D在线段PQ上，且DQ=DC．求证：CD是⊙O的切线；
（2）若sin∠Q=
| 3 |
| 5 |
考点：切线的判定,解直角三角形
专题：
分析：（1）如图，连结OC．欲证明CD是⊙O的切线，只需证得CD⊥OC即可；
（2）如图，作OH⊥BC，H为垂足．通过解Rt△BQP和在Rt△BHO中，可以求得BQ=10、BH=
．然后由等腰三角形“三线合一”的性质得到BC=2BH=2×
=
，则CQ=BQ-BC=
．
（2）如图，作OH⊥BC，H为垂足．通过解Rt△BQP和在Rt△BHO中，可以求得BQ=10、BH=
| 12 |
| 5 |
| 12 |
| 5 |
| 24 |
| 5 |
| 26 |
| 5 |
解答：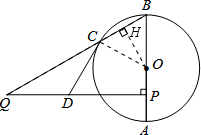
解：（1）如图，连结OC．
∵DQ=DC，
∴∠Q=∠QCD．
∵OC=OB，
∴∠B=∠OCB．
∵QP⊥BP，
∴∠QPB=90° 即∠B+∠Q=90°，
∴∠QCD+∠OCB=90°，
∴∠OCD=90°，
∴CD⊥OC，即CD是⊙O的切线；
（2）如图，作OH⊥BC，H为垂足．
∵BP=6，AP=2，
∴AB=8，OB=
AB=4．
在Rt△BQP中，sinQ=
=
=
，
∴BQ=10，cos∠B=sin∠Q=
在Rt△BHO中，cos∠B=
=
=
，
∴BH=
．
∵OH⊥BC，
∴BC=2BH=2×
=
，
∴CQ=BQ-BC=
．
（法二：连结AC，证△ABC∽△QBP，得
=
，
=
，BC=
∴CQ=BQ-BC=
）．
解：（1）如图，连结OC．∵DQ=DC，
∴∠Q=∠QCD．
∵OC=OB，
∴∠B=∠OCB．
∵QP⊥BP，
∴∠QPB=90° 即∠B+∠Q=90°，
∴∠QCD+∠OCB=90°，
∴∠OCD=90°，
∴CD⊥OC，即CD是⊙O的切线；
（2）如图，作OH⊥BC，H为垂足．
∵BP=6，AP=2，
∴AB=8，OB=
| 1 |
| 2 |
在Rt△BQP中，sinQ=
| BP |
| BQ |
| 6 |
| BQ |
| 3 |
| 5 |
∴BQ=10，cos∠B=sin∠Q=
| 3 |
| 5 |
在Rt△BHO中，cos∠B=
| BH |
| BO |
| BH |
| 4 |
| 3 |
| 5 |
∴BH=
| 12 |
| 5 |
∵OH⊥BC，
∴BC=2BH=2×
| 12 |
| 5 |
| 24 |
| 5 |
∴CQ=BQ-BC=
| 26 |
| 5 |
（法二：连结AC，证△ABC∽△QBP，得
| BC |
| BP |
| AB |
| BQ |
| BC |
| 6 |
| 8 |
| 10 |
| 24 |
| 5 |
| 26 |
| 5 |
点评：本题考查了切线的判定和解直角三角形的应用，切线的判定定理是：过半径的外端点与半径垂直的直线为圆的切线．也考查圆周角定理的推论以及解直角三角形．
练习册系列答案
相关题目
下列计算正确的是（ ）
| A、3ab-2ab=1 | ||||
B、（
| ||||
| C、-（-a）4÷a2=a2 | ||||
D、（
|
已知在Rt△ABC中，∠C=90°，AB=13，AC=12，则∠B的余弦值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，已知∠A=4∠B=104°，则∠C的度数是（ ）
| A、50° | B、45° |
| C、40° | D、30° |
如图，AB是⊙O的直径，点E是