题目内容
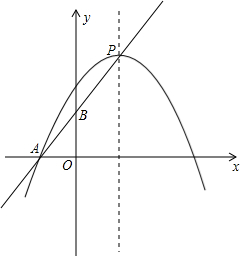 已知直线y=kx+3-k,当k=1,k=
已知直线y=kx+3-k,当k=1,k=| 3 |
| 2 |
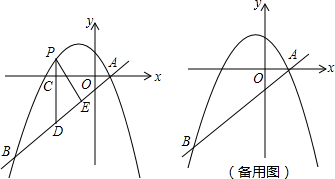
(1)求定点P的坐标;
(2)若k=
| 3 |
| 2 |
(3)若k≠
| 3 |
| 2 |
考点:二次函数综合题
专题:
分析:(1)分别将k=1,k=
代入求出两函数解析式,进而得出其交点坐标;
(2)利用顶点式求出函数解析式即可;
(3)根据①当AB为平行四边形的边时,则DE由AB平移所得,②当AB为平行四边形的对角线时分别求出符合题意的值即可.
| 3 |
| 2 |
(2)利用顶点式求出函数解析式即可;
(3)根据①当AB为平行四边形的边时,则DE由AB平移所得,②当AB为平行四边形的对角线时分别求出符合题意的值即可.
解答:解:(1)当k=1,k=
时,
,
解得:
,
所以P点坐标为(1,3);
(2)当k=
时,求得A(-1,0),B(0,
)
设以点P(1,3)为顶点的抛物线为y=a(x-1)2+3,
将A(-1,0)代入y=a(x-1)2+3,
得a=-
所以,抛物线解析式为y=-
(x-1)2+3(或y=-
x2+
x+
);
(3)①当AB为平行四边形的边时,则DE由AB平移所得,
i)若A平移至D,则B平移至E(如图1)
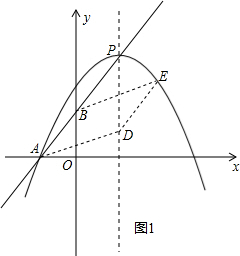
由对称轴为直线x=1,可知D横坐标为1,
又∵A(-1,0),B(0,
),可知E横坐标为2
将x=2代入y=-
(x-1)2+3,得y=
∴E坐标为(2,
)
把E坐标为(2,
)代入y=kx+3-k,得k=-
,
ii)若A平移至E,则B平移至D(如图2)
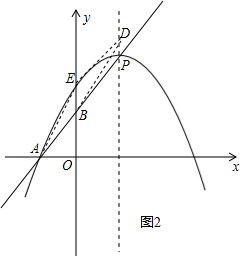
由对称轴为直线x=1,可知D横坐标为1,
又∵A(-1,0),B(0,
),可知E横坐标为0
将x=0代入y=-
(x-1)2+3,得y=
∴E坐标为(0,
)
把E坐标为(0,
)代入y=kx+3-k,得k=
,
②当AB为平行四边形的对角线时(如图3)
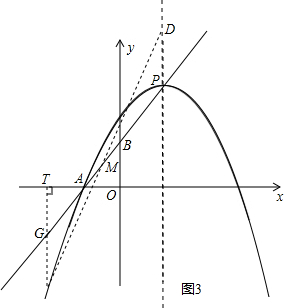
AB与DE交于点M,则M是AB中点,也是DE中点
又∵A(-1,0),B(0,
),可知M坐标为(-
,
)
∵可知D横坐标为1,所以E横坐标为-2
将x=-2代入y=-
(x-1)2+3,得y=-
∴E坐标为(-2,-
)
把E坐标为(-2,-
)代入y=kx+3-k,得k=
,
综上知,k=-
,
,
时,以A、B、E、D为顶点的四边形是平行四边形.
(注:其它合理解法,酌情给分)
| 3 |
| 2 |
|
解得:
|
所以P点坐标为(1,3);
(2)当k=
| 3 |
| 2 |
| 3 |
| 2 |
设以点P(1,3)为顶点的抛物线为y=a(x-1)2+3,
将A(-1,0)代入y=a(x-1)2+3,
得a=-
| 3 |
| 4 |
所以,抛物线解析式为y=-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
(3)①当AB为平行四边形的边时,则DE由AB平移所得,
i)若A平移至D,则B平移至E(如图1)

由对称轴为直线x=1,可知D横坐标为1,
又∵A(-1,0),B(0,
| 3 |
| 2 |
将x=2代入y=-
| 3 |
| 4 |
| 9 |
| 4 |
∴E坐标为(2,
| 9 |
| 4 |
把E坐标为(2,
| 9 |
| 4 |
| 3 |
| 4 |
ii)若A平移至E,则B平移至D(如图2)

由对称轴为直线x=1,可知D横坐标为1,
又∵A(-1,0),B(0,
| 3 |
| 2 |
将x=0代入y=-
| 3 |
| 4 |
| 9 |
| 4 |
∴E坐标为(0,
| 9 |
| 4 |
把E坐标为(0,
| 9 |
| 4 |
| 3 |
| 4 |
②当AB为平行四边形的对角线时(如图3)

AB与DE交于点M,则M是AB中点,也是DE中点
又∵A(-1,0),B(0,
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
∵可知D横坐标为1,所以E横坐标为-2
将x=-2代入y=-
| 3 |
| 4 |
| 15 |
| 4 |
∴E坐标为(-2,-
| 15 |
| 4 |
把E坐标为(-2,-
| 15 |
| 4 |
| 9 |
| 4 |
综上知,k=-
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 4 |
(注:其它合理解法,酌情给分)
点评:此题主要考查了二次函数综合以及平行四边形的判定与性质以及待定系数法求函数解析式等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
一个圆锥的侧面展开图是一个圆心角为216°,面积为60π的扇形,则这个圆锥的高是( )
| A、8 | B、10 | C、12 | D、14 |
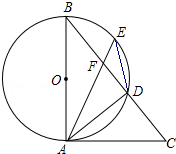 如图,AB是⊙O的直径,点E是
如图,AB是⊙O的直径,点E是
 如图,某登山队在山脚A处测得山顶B处的仰角为45°,沿坡角30°的斜坡AD前进1000m后到达D处,又测得山顶B处的仰角为60°.求山的高度BC.
如图,某登山队在山脚A处测得山顶B处的仰角为45°,沿坡角30°的斜坡AD前进1000m后到达D处,又测得山顶B处的仰角为60°.求山的高度BC.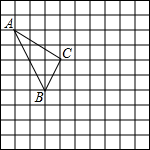 在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2).
在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2).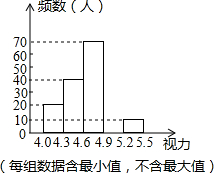 某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
某区对参加2014年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题: