题目内容
 已知点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,求证:△AOD≌△BOC.
已知点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,求证:△AOD≌△BOC.考点:矩形的性质,全等三角形的判定与性质
专题:证明题
分析:根据矩形的对边相等可得AD=BC,根据矩形的对边平行可得AD∥BC,根据两直线平行,内错角相等可得∠E=∠OBC,再求出BC=DE,然后利用“角角边”证明△AOD和△BOC全等即可.
解答:证明:在矩形ABCD中,AD=BC,AD∥BC,
∴∠E=∠OBC,
∵AD=DE,
∴BC=DE,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(AAS).
∴∠E=∠OBC,
∵AD=DE,
∴BC=DE,
在△AOD和△BOC中,
|
∴△AOD≌△BOC(AAS).
点评:本题考查了矩形的性质,全等三角形的判定,熟练掌握矩形的对边平行且相等找出三角形全等的条件是解题的关键.

练习册系列答案
相关题目
已知在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠B的余弦值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
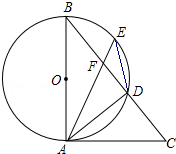 如图,AB是⊙O的直径,点E是
如图,AB是⊙O的直径,点E是
 已知:如图,正方形ABCD,E,F分别为DC,BC中点.
已知:如图,正方形ABCD,E,F分别为DC,BC中点.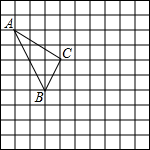 在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2).
在如图的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,4),(-1,2). 如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西30°方向上,BP的距离为30海里.
如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西30°方向上,BP的距离为30海里.