Question

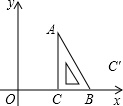如图，把一块含有30°角的直角三角尺放置在平面直角坐标系中，BC边落在x轴的正半轴上，点A在第一限象内，∠ACB=90°，∠CAB=30°，AC=4

3

，沿着AB翻折三角尺，直角顶点C落在C′处．设A、C′两点的横坐标分别为m、n．
（1）试用m的代数式表示n；
（2）若反比例函数y=

k

x

（x＞0）的图象恰好经过A、C′两点，求k的值．

Answer 1

考点：翻折变换（折叠问题）,反比例函数图象上点的坐标特征

专题：

分析：（1）过点C′作C′D⊥x轴于D．在Rt△ACB中，根据三角函数可求BC，在Rt△C′DB中，根据翻折的性质和三角函数可求BD，由于OD=OC+BC+BD，依此可用m的代数式表示n；
（2）因为反比例函数y=

k

x

（x＞0）的图象恰好经过A、C′两点，依此可得关于k，m的方程组，解方程组即可求解．

解答：解：（1）过点C′作C′D⊥x轴于D．
在Rt△ACB中，∠ACB=90°，∠CAB=30°，AC=4

3

，
∴∠C′BA=∠CBA=60°，BC=BC′=AC•tan30°=4，
∵∠C′BD=180°-60°-60°=60°，
在Rt△C′DB中，BD=BC′•cos60°=2，C′D=BC′•sin60°=2

3

，
∵OD=OC+BC+BD，
∴n=m+4+2=m+6；

（2）∵反比例函数y=

k

x

（x＞0）的图象恰好经过A、C′两点，
∴

k m =4 3 k m+6 =2 3

，
解得

k=24 3 m=6

．
故k的值是24

3

．

点评：本题综合考查了翻折变换（折叠问题）、反比例函数图象上点的坐标特征、三角函数的知识，以及方程思想．