题目内容
20.在△ABC中,∠BAC=90°,AB=AC.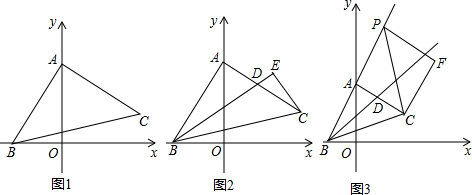
(1)如图1,若A、B两点的坐标分别是A(0,4),B(-2,0),求C点的坐标;
(2)如图2,作∠ABC的角平分线BD,交AC于点D,过C点作CE⊥BD于点E,求证:CE=$\frac{1}{2}$BD;
(3)如图3,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点,当点P运动时,点Q是否恒在射线BD上?若在,请证明;若不在,请说明理由.
分析 (1)要求点C坐标,作CM⊥AO,只要利用全等三角形的性质求出OM、CM即可;
(2)延长CE、BA相交于点F.可以证明Rt△ABD≌Rt△ACF,再证明△BCE≌△BFE得到CE=EF,就可以得出结论;
(3)点Q是否恒在射线BD上,只要证明QM=QN,只要证明△M,HQ≌△NGQ即可.
解答 解: (1)如图1中,作CM⊥OA垂足为M,
(1)如图1中,作CM⊥OA垂足为M,
∵∠AOB=∠BAC=90°,
∴∠BAO+∠CAM=90°,∠BAO+∠ABO=90°,
∴∠ABO=∠CAM,
在△ABO和△CAM中,
$\left\{\begin{array}{l}{∠ABO=∠CAM}\\{∠AOB=∠AMC}\\{AB=AC}\end{array}\right.$,
∴△ABO≌△CAM,
∴MC=AO=4,AM=BO=2,MO=AO-AM=2,
∴点C坐标(4,2);
(2)如图2,延长CE、BA相交于点F,
∵∠EBF+∠F=90°,∠ACF+∠F=90°,
∴∠EBF=∠ACF,
在△ABD和△ACF中$\left\{\begin{array}{l}{∠EBF=∠ACF}\\{AB=AC}\\{∠BAC=∠CAF}\end{array}\right.$,
∴△ABD≌△ACF(ASA),
∴BD=CF,
在△BCE和△BFE中,$\left\{\begin{array}{l}{∠EBF=∠CBE}\\{BE=BE}\\{∠CEB=∠FEB}\end{array}\right.$,
∴△BCE≌△BFE(ASA),
∴CE=EF,
∴CE=$\frac{1}{2}$BD;
(3)结论:点Q恒在射线BD上,
理由如下:
如图3中作QE⊥PF,QG⊥FC,QH⊥PC,QM⊥BP,QN⊥BC,垂足分别为E、G、H、M、N.
在四边形QMBN中,∵∠QMB=∠QNB=90°,
∴∠MQN=180°-∠ABC=135°,
同理可证:∠HQG=135°,
∴∠MQN=∠HQG,
∴∠MQH=∠GQN,
∵PQ平分∠FPC,QF平分∠PFC,QE⊥PF,QH⊥PC,QG⊥FC,
∴QE=QH=QG,∠QPH=$\frac{1}{2}$∠CPF=22.5°,
∵∠PMQ=∠PHQ=90°,
∴M、H、Q、P四点共圆,
∴∠HMP=∠HPQ=22.5°,同理∠QNG=22.5°,
∴∠FMQ=∠QNG,
在△MHQ和△NGQ中,
$\left\{\begin{array}{l}{∠HMQ=∠QNG}\\{∠MQH=∠NQG}\\{QF=QG}\end{array}\right.$,
∴△MHQ≌△NGQ,
∴QM=QN,
∵QM⊥BP,QN⊥BC,
∴BQ平分∠ABC,
∴点Q恒在射线BD上.
点评 本题考查了全等三角形的判定或性质、等腰直角三角形的性质、坐标与图形的性质、四点共圆等知识,关键是构造全等三角形,过点Q向两边作垂线是证明角平分线的常用手段.

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案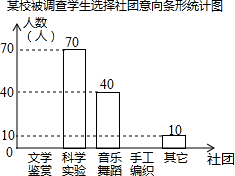 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):| 选择意向 | 所占百分比 |
| 文学鉴赏 | a |
| 科学实验 | 35% |
| 音乐舞蹈 | b |
| 手工编织 | 10% |
| 其他 | c |
(1)本次调查的学生总人数为200人;
(2)补全条形统计图;
(3)将调查结果绘成扇形统计图,则“音乐舞蹈”社团所在扇形所对应的圆心角为72°;
(4)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数为420人.
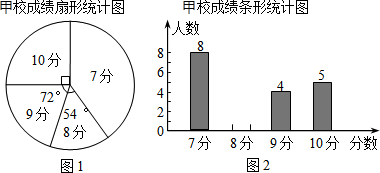 甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表
甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表乙校成绩统计表
| 分数 | 7分 | 8分 | 9分 | 10分 |
| 人数 | 11 | 0 | 8 |
(2)请将图2的统计图和乙校成绩统计表补充完整;
(3)成绩最好的男同学王东、李亮.女同学张梅、萧红被选中参加电视辩论,辩论前抽签决定每两人为一组,请你用树状图和列表法表示所有可能的分组结果,并计算两名男同学恰好在同一组的概率.
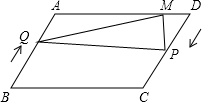 已知在?ABCD中,AB=20cm,AD=30cm,∠ABC=60°,点Q从点B出发沿BA向点A匀速运动,速度为2cm/s,同时点P从点D出发沿DC匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,过点P做PM⊥AD于点M,连接PQ、QM.设运动的时间为ts(0<t≤6).
已知在?ABCD中,AB=20cm,AD=30cm,∠ABC=60°,点Q从点B出发沿BA向点A匀速运动,速度为2cm/s,同时点P从点D出发沿DC匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,过点P做PM⊥AD于点M,连接PQ、QM.设运动的时间为ts(0<t≤6).