题目内容
12.(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某人.请画树状图或列表求第二次传球后球回到甲手里的概率.(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是$\frac{n-1}{{n}^{2}}$.(请直接写出结果)
分析 (1)根据画树状图,可得总结果与传到甲手里的情况,根据传到甲手里的情况比上总结过,可得答案;
(2)根据第一步传的结果是n,第二步传的结果是n2,第三步传的结果是总结过是n3,传给甲的结果是n(n-1),根据概率的意义,可得答案.
解答 解:(1)画树状图:
共有9种等可能的结果,其中符合要求的结果有3种,
∴P(第2次传球后球回到甲手里)=$\frac{3}{9}$=$\frac{1}{3}$.
(2)第三步传的结果是n3,传给甲的结果是n(n-1),
第三次传球后球回到甲手里的概率是$\frac{n(n-1)}{{n}^{3}}$=$\frac{n-1}{{n}^{2}}$,
故答案为:$\frac{n-1}{{n}^{2}}$.
点评 本题考查了树状图法计算概率,计算概率的方法有树状图法与列表法,正确的画出树状图是解题关键.

练习册系列答案
相关题目
1.某市某中学为了搞好“创建全国文明城市”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A,B,C,D,E五个组,x表示测试成绩).通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.

调查测试成绩分组表
请你根据图中提供的信息解答以下问题:
(1)参加调查测试的学生为400人;
(2)将条形统计图补充完整;
(3)本次调查测试成绩的中位数落在C组内;
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2 600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.

调查测试成绩分组表
| A组:90≤x≤100 |
| B组:80≤x<90 |
| C组:70≤x<80 |
| D组:60≤x<70 |
| E组:x<60 |
(1)参加调查测试的学生为400人;
(2)将条形统计图补充完整;
(3)本次调查测试成绩的中位数落在C组内;
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2 600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.
2.一组数据8,3,8,6,7,8,7的众数和中位数分别是( )
| A. | 8,6 | B. | 7,6 | C. | 7,8 | D. | 8,7 |
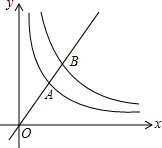 如图,在平面直角坐标系中,O为原点,直线y=kx(k>0)与双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)分别交于A,B两点,则$\frac{OB}{OA}$=$\sqrt{2}$.
如图,在平面直角坐标系中,O为原点,直线y=kx(k>0)与双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)分别交于A,B两点,则$\frac{OB}{OA}$=$\sqrt{2}$.