题目内容
1. 如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )
如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{7}$ | C. | $\frac{12}{5}$ | D. | $\frac{5}{2}$ |
分析 根据已知条件得到AB=7,根据相似三角形的判定和性质即可得到结论.
解答 解:∵AD=3,BD=4,
∴AB=7,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$,即$\frac{3}{7}$=$\frac{DE}{5}$,
∴DE=$\frac{15}{7}$,
故选B.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在利用相似三角形的性质时主要利用相似比计算线段的长.

练习册系列答案
相关题目
12.关于x的方程(a+3)x2-5x=0的解的情况是( )
| A. | 一个解 | B. | 两个解 | C. | 一个或两个解 | D. | 无解 |
6.下列事件是必然事件的是( )
| A. | 车辆随机到达一个路口,遇到红灯 | |
| B. | 两条线断可以组成一个三角形 | |
| C. | 400人中有两个人的生日在同一天 | |
| D. | 掷一枚质地均匀的骰子,掷出的点数是质数 |
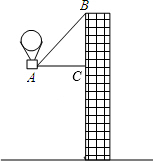 如图,有一热气球到达A处时,仪器显示其正前方一高楼顶部B的仰角是43°,与楼的水平距离AC为12米,为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)
如图,有一热气球到达A处时,仪器显示其正前方一高楼顶部B的仰角是43°,与楼的水平距离AC为12米,为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)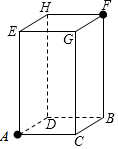 一只蚂蚁如果沿长方体的表面从A点爬到F点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.
一只蚂蚁如果沿长方体的表面从A点爬到F点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.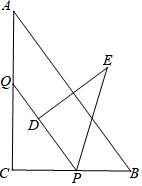 如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.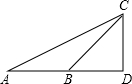 如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A,B两处的视角∠ACB是多少度?
如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A,B两处的视角∠ACB是多少度?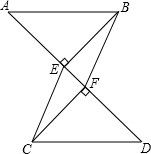 如图,已知AB∥CD,BE⊥AD于点E,CF⊥AD于点F,且AF=DE,求证:四边形BECF是平行四边形.
如图,已知AB∥CD,BE⊥AD于点E,CF⊥AD于点F,且AF=DE,求证:四边形BECF是平行四边形.