题目内容
20. 在如图所示的正方形网格中,每个小正方形的边长均为1,△ABC的顶点A、C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长均为1,△ABC的顶点A、C的坐标分别为(-4,5),(-1,3).(1)请在如图所示的网格平面内画出平面直角坐标系,并写出点B的坐标.
(2)请把△ABC先向右移5个单位长度,再向下移3个单位长度,得到△A′B′C′,请在图中画出△A′B′C′.
(3)求△A′B′C′的面积.
分析 (1)根据点C的坐标,即可找出x、y轴的位置,以此建立直角坐标系即可;
(2)找出点A、B、C平移后的点A′、B′、C′,将其两两相连即可;
(3)由△A′B′C′的面积等于矩形的面积减去三个小三角线的面积,即可求出△A′B′C′的面积.
解答 解:(1)如图所示建立直角坐标系,点B的坐标为(-2,1).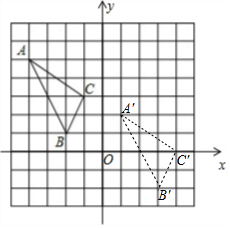
(2)依照题意平移△ABC,得到△A′B′C′,如图所示.
(3)S△A′B′C′=3×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×3×2-$\frac{1}{2}$×1×2=4.
点评 本题考查了作图中的平移变换以及三角形的面积,解题的关键是:(1)根据点B的坐标确定x、y轴的位置;(2)找出点A、B、C平移后的点A′、B′、C′;(3)利用分割图形法求△A′B′C′的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
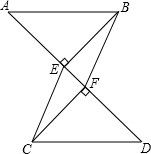 如图,已知AB∥CD,BE⊥AD于点E,CF⊥AD于点F,且AF=DE,求证:四边形BECF是平行四边形.
如图,已知AB∥CD,BE⊥AD于点E,CF⊥AD于点F,且AF=DE,求证:四边形BECF是平行四边形.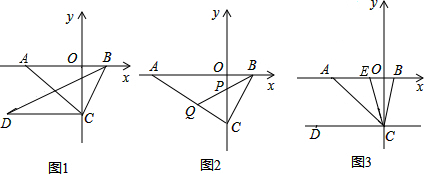
 如图,如果$\frac{AB}{BC}=\frac{DE}{EF}$,那么AD∥BE∥CF,这个命题是真命题(填“真”或“假”).
如图,如果$\frac{AB}{BC}=\frac{DE}{EF}$,那么AD∥BE∥CF,这个命题是真命题(填“真”或“假”). 如图,点A,B的坐标分别为(1,0),(0,2),若将线段AB平移到A1B1的坐标分别为(2,a),(b,3),试求a2-2b的值.
如图,点A,B的坐标分别为(1,0),(0,2),若将线段AB平移到A1B1的坐标分别为(2,a),(b,3),试求a2-2b的值. 填空完成推理过程:
填空完成推理过程: