题目内容
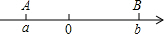 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:①数轴上表示1和3两点之间的距离是
②数轴上表示x和-1的两点之间的距离表示为
③若|x-2|+|x+4|=6,则符合条件的非正整数x有
④由以上探索猜想,对于任何有理数x,则|x+1|+|x-3|是否有最小值?若有,写出最小值;如果没有,说明理由.
考点:数轴,绝对值
专题:
分析:①根据两点之间距离的求法求解即可;
②根据两点之间距离的求法求解即可,|x-(-1)|=|x+1|;
③分三种情况:x≤-4,-4<x<2,x≥2时分别计算,进而求解;
④根据绝对值的性质去掉绝对值号,然后计算即可得解.
②根据两点之间距离的求法求解即可,|x-(-1)|=|x+1|;
③分三种情况:x≤-4,-4<x<2,x≥2时分别计算,进而求解;
④根据绝对值的性质去掉绝对值号,然后计算即可得解.
解答:解:①3-1=2,2-(-5)=7;
②|x-(-1)|=|x+1|;
③分三种情况:当x≤-4时,|x-2|+|x+4|=2-x-x-4=-2x-2,
则-2x-2=6,解得x=-4;
当-4<x<2时,|x-2|+|x+4|=2-x+x+4=6,
当x≥2时,|x-2|+|x+4|=x-2+x+4=2x+2,
2x+2=6,解得x=2,不合题意舍去;
∴符合条件的非正整数x有-4;-3;-2;-1;0;
④当x<-1时,|x+1|+|x-3|=-1-x-x+3=-2x+2,
当-1≤x≤3时,|x+1|+|x-3|=1+x-x+3=4,
当x>3时,|x+1|+|x-3|=x+1+x-3=2x-2,
在数轴上|x+1|+|x-3|的几何意义是:表示有理数x的点到-3及到1的
距离之和,所以当-3≤x≤1时,它取得最小值为4.
故答案为:(1)2;7 (2)|x-(-1)|(3)-4,-3,-2,-1,0 (4)有最小值4.
②|x-(-1)|=|x+1|;
③分三种情况:当x≤-4时,|x-2|+|x+4|=2-x-x-4=-2x-2,
则-2x-2=6,解得x=-4;
当-4<x<2时,|x-2|+|x+4|=2-x+x+4=6,
当x≥2时,|x-2|+|x+4|=x-2+x+4=2x+2,
2x+2=6,解得x=2,不合题意舍去;
∴符合条件的非正整数x有-4;-3;-2;-1;0;
④当x<-1时,|x+1|+|x-3|=-1-x-x+3=-2x+2,
当-1≤x≤3时,|x+1|+|x-3|=1+x-x+3=4,
当x>3时,|x+1|+|x-3|=x+1+x-3=2x-2,
在数轴上|x+1|+|x-3|的几何意义是:表示有理数x的点到-3及到1的
距离之和,所以当-3≤x≤1时,它取得最小值为4.
故答案为:(1)2;7 (2)|x-(-1)|(3)-4,-3,-2,-1,0 (4)有最小值4.
点评:本题考查了数轴,绝对值的性质,理解数轴上两点间的距离的表示和采用数形结合的思想是解题的关键.

练习册系列答案
相关题目
如果把分式
中的x、y同时缩小为原来的一半,则分式的值( )
| xy |
| 2x+3y |
| A、不变 |
| B、缩小为原来的一半 |
| C、缩小为原来的四分之一 |
| D、扩大为原来的2倍 |
下列方程中,是关于x的一元二次方程的是( )
| A、3(x+1)2=2(x+1) | ||||
B、
| ||||
| C、ax2+bx+c=0 | ||||
| D、x2-2x=x2+1 |
 将一副三角板如图所示放在一起,连接AD,则∠ADB的正切值是
将一副三角板如图所示放在一起,连接AD,则∠ADB的正切值是