题目内容
若抛物线y=-x2+2x+8与x轴交于B、C两点,点D平分BC,点A为抛物线上的点,且∠BAC为锐角,则点A横坐标的取值范围为 .
考点:抛物线与x轴的交点
专题:
分析:由“∠BAC为锐角”可知点A在以定线段BC为直径的圆外,又由点A为抛物线上的点,从而可确定动点A的取值范围.
解答: 解:如图,∵y=-x2+2x+8,
解:如图,∵y=-x2+2x+8,
∴当y=0时,-x2+2x+8=0,
解得x=-2或4,
即抛物线与x轴交于两点B(-2,0)、C(4,0).
以BC为直径作⊙D,则⊙D与抛物线交于两点P(1-2
,1)、Q(1+2
,1).
当点A在⊙D外时,∠BAC<90°,
则A的横坐标取值范围是x<-2或1-2
<x<1+2
或x>4.
故答案为:x<-2或1-2
<x<1+2
或x>4.
 解:如图,∵y=-x2+2x+8,
解:如图,∵y=-x2+2x+8,∴当y=0时,-x2+2x+8=0,
解得x=-2或4,
即抛物线与x轴交于两点B(-2,0)、C(4,0).
以BC为直径作⊙D,则⊙D与抛物线交于两点P(1-2
| 2 |
| 2 |
当点A在⊙D外时,∠BAC<90°,
则A的横坐标取值范围是x<-2或1-2
| 2 |
| 2 |
故答案为:x<-2或1-2
| 2 |
| 2 |
点评:此题主要考查了抛物线与x轴的交点,解题时首先求出抛物线与x轴的交点坐标,然后利用已知条件探究即可解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC中,DE∥BC,
如图,△ABC中,DE∥BC, 如图,Rt△ABC中,斜边AB上一点M,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:4,求MN的长.
如图,Rt△ABC中,斜边AB上一点M,MN⊥AB交AC于N,若AM=3cm,AB:AC=5:4,求MN的长. 如图,AB⊥BF,MC⊥BF,NE⊥BF,且CD=1,CE=3,EF=2,MC=NE=1.5,则AB=
如图,AB⊥BF,MC⊥BF,NE⊥BF,且CD=1,CE=3,EF=2,MC=NE=1.5,则AB=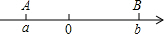 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题: