题目内容
在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,a、b是关于x的方程x2-7x+c+7=0的两根,求AB边上的中线长.
考点:一元二次方程的应用,根与系数的关系,直角三角形斜边上的中线,勾股定理
专题:
分析:由于a、b是关于x的方程x2-7x+c+7=0的两根,由根与系数的关系可知:a+b=7,ab=c+7;由勾股定理可知:a2+b2=c2,则(a+b)2-2ab=c2,即49-2(c+7)=c2,由此求出c,再根据直角三角形斜边中线定理即可得中线长.
解答:解:∵a、b是关于x的方程x2-7x+c+7=0的两根,
∴根与系数的关系可知:a+b=7,ab=c+7;
由直角三角形的三边关系可知:a2+b2=c2,
则(a+b)2-2ab=c2,
即49-2(c+7)=c2,
解得:c=5或-7(舍去),
再根据直角三角形斜边中线定理得:中线长为
.
答:AB边上的中线长是
.
∴根与系数的关系可知:a+b=7,ab=c+7;
由直角三角形的三边关系可知:a2+b2=c2,
则(a+b)2-2ab=c2,
即49-2(c+7)=c2,
解得:c=5或-7(舍去),
再根据直角三角形斜边中线定理得:中线长为
| 5 |
| 2 |
答:AB边上的中线长是
| 5 |
| 2 |
点评:本题考查三角形斜边中线长定理及一元二次方程根与系数的关系运用,勾股定理的运用,一元二次方程的解法的运用,解答时运用一元二次方程的根与系数的关系建立方程是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
下列命题中,逆命题是真命题的是( )
| A、若a2=b2,则a=b |
| B、全等三角形的周长相等 |
| C、对顶角相等 |
| D、个位上的数字为0的整数能被5整除 |
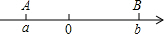 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
 已知如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠DAC=100°,则∠BAC=
已知如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠DAC=100°,则∠BAC=