题目内容
 将一副三角板如图所示放在一起,连接AD,则∠ADB的正切值是
将一副三角板如图所示放在一起,连接AD,则∠ADB的正切值是考点:解直角三角形
专题:
分析:连结AD,作AE⊥BD,交DB的延长线于点E,设AE为1,得到DE的值,相除即可.
解答: 解:如图,连结AD,作AE⊥BD,交DB的延长线于点E.
解:如图,连结AD,作AE⊥BD,交DB的延长线于点E.
由题意可得:∠ABE=∠CBD=45°,
设AE=1,则AB=
,
∴BC=
,
∵Rt△BCD是等腰直角三角形,
∴BD=
,
∴DE=1+
,
∴tan∠ADB=1÷(
+1)=
.
故答案为
.
 解:如图,连结AD,作AE⊥BD,交DB的延长线于点E.
解:如图,连结AD,作AE⊥BD,交DB的延长线于点E.由题意可得:∠ABE=∠CBD=45°,
设AE=1,则AB=
| 2 |
∴BC=
| 6 |
∵Rt△BCD是等腰直角三角形,
∴BD=
| 3 |
∴DE=1+
| 3 |
∴tan∠ADB=1÷(
| 3 |
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题考查解直角三角形的知识;构造出所求角所在的直角三角形是解决本题的难点.

练习册系列答案
相关题目
已知正n边形的一个外角与一个内角的比为1﹕3,则n等于( )
| A、4 | B、6 | C、8 | D、12 |
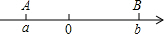 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题: 在图中,原点O是△ABC和△A1B1C1的位似中心,△ABC三个顶点坐标分别为A(6,6)、B(8,4)、C(4,0)是点C的对应点,且点C1的横坐标为2.
在图中,原点O是△ABC和△A1B1C1的位似中心,△ABC三个顶点坐标分别为A(6,6)、B(8,4)、C(4,0)是点C的对应点,且点C1的横坐标为2.